注意:この記事自体は、SEOに関するアドバイスについて多くを述べるものではない。ただ、僕らがPageStrengthという指標を考え出した経緯について、技術的な背景を詳しく説明するとともに、間もなくリリース予定の新ツールをこっそり紹介しようと思う。
追加情報:ここで紹介するツールは、僕以外の開発スタッフであるJeff、Mel、Mike、Timmyたちの仕事だと言った方がいいだろう。僕がこういうブログ記事を書く作業などに手を取られている間、みんなは膨大な時間を開発に注ぎ込んだ。
ここで述べられている内容は、すでにPageStrengthチェッカーの後継となるTrifecta Tool Setというツールとして、SEOmozのメンバー向けに公開されている。
SEOmozでは現在、開発に懸命に取り組んでいる新ツールがある(初期段階のスクリーンショットをここでお見せする!)。このツールでやろうとしていることの1つは、すでにいただいているアドバイスを取り入れることだ。
以前のSMX Advancedでは、SEO担当者と検索エンジン関係者の双方から、データに焦点を合わせるべきであり、検索順位のチェックだけに終始するのはどうか止めてほしいという言葉をいただいた。そこで僕らは数字に取り組んできた――それはもうたくさんの数字に。
こうしたデータについては、ちょっとばかり解釈に苦しむような場面もあり、そこでデータを理解するために回帰分析をはじめとするデータ処理を利用した。実をいうとそのために、オンライン回帰分析ツールを急きょ準備したんだ。
僕らが理解しようとしている問題を、下の図に示す。
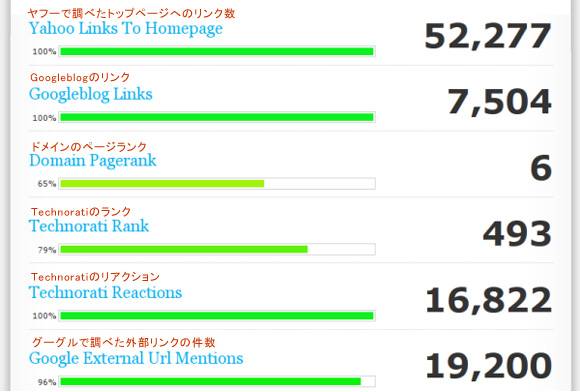
非常に信頼度が高い複数の情報源からすばらしいデータを集めていることがわかってもらえると思う。ただ、右側の数字に注目すると、尺度がそれぞれ異なっていることに気が付くだろう。そしてこうした数的指標について少しでも知っている人なら、URLの出現回数5回と50回との差が、2万5回と2万50回との差とは大きく違うことを心得ているはずだ。
ここではグーグルを使って調べたドメイン言及回数の重要性を理解したいとする。ウェブ上でドメインが数多く言及されれば、おそらくは検索順位におけるそのドメインの強さと影響力も大きくなる。だが、そのことをもっと正確に判断するにはどうすればいいだろうか? 言及された回数が100回あれば十分なのか? 1000回から1100回へ増えたら、大きな増加だと言えるのか? どのあたりが10%で、どのあたりが90%なのか?
SEOに精通した人なら、いくつかの事例を示すことができるだろう(実のところ、僕が知る限り、そんなことができるのは米国にはほんの数人いるだけだし、米国外にもわずかしかいない)。
少し例をみてみよう。
| グーグルで調べた そのドメイン名の 言及回数 | 評価スコア |
|---|---|
| 1890000 | 100 |
| 1280000 | 100 |
| 866000 | 100 |
| 659000 | 96 |
| 584000 | 94 |
| 247000 | 80 |
| 115000 | 65 |
| 32500 | 45 |
| 13400 | 30 |
| 11300 | 28 |
| 6590 | 15 |
| 218 | 5 |
| 4 | 1 |
数値の基になったサイトは伏せてあるが、これは無関係なところに迷惑をかけないためだ(^_-)。だけど、どういうデータかはわかるだろう。評価の基準がすでにある程度わかっている実際の例を示してみた。
この表では、ほかの条件が同じならば、出現回数86万6000回以上はすべて評価スコアが満点の100としている。また、出現回数がどのくらいなら評価スコアがいくつになるかも示してある。ここでの知りたいのは、新規データの評価スコアをどう計算すればいいかということだ。ここで回帰分析が登場する。
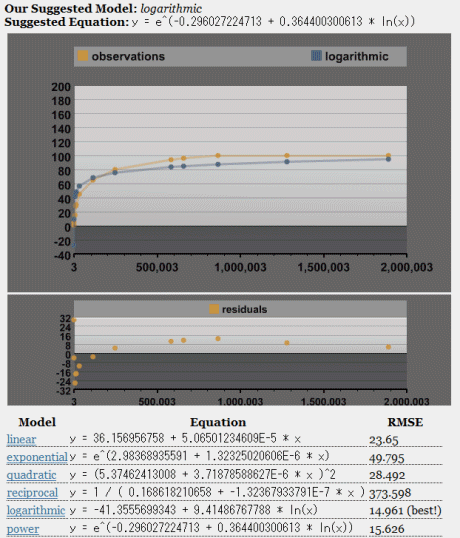
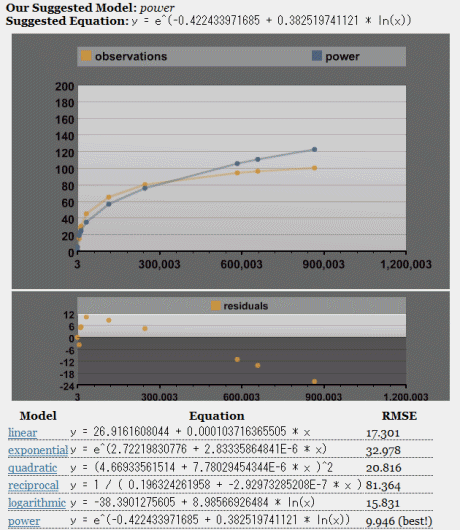
考え方としては、実測値(この場合は、優秀なSEO担当者が直観的に判断したものだが)のパターンに適合する回帰式、つまりモデルを見つけ出そうというものだ。このデータに関して、僕のツールがはじき出したモデルを見てもらいたい。
最適モデルに加えて、グラフを2つ載せてある。回帰分析を行ったことがある人なら、自分のデータと適用したモデルを視覚化して感覚的に比較することの重要性を知っているはずだ。モデルによる推定値の誤差を示す「残差」のグラフも載せてある。たとえば、ドメイン名の出現回数が24万7000回なら、実際の評価スコアが80%でモデルの推定値は75.55%だから、残差は4.45ポイントとなる。統計上は、残差の2乗を考えると役に立つことが多い(右側の表には「residual sq(残差平方)」の欄がある)。残差平方には、大きい誤差ほど目立つという効果もある。
入門編はここまでにして、さらに高度な内容に移ろう。ここで取り上げたデータの場合(先ほどの「モデル」は新しいタブで開いておこう)、実測値の上限が100%であることにお気づきだろう。満点を100としたのは恣意的なもので、単純なモデル化手法においては数学的な問題が少しばかり生じる。また、最適モデルでは、グラフの中央部分であまりうまく予測できていないことがわかると思う。そこで、コツをいくつかを紹介する。
ここで取り上げた100%モデルのように上限値のある尺度を使用する場合は、モデルに上限値を超える部分まで予測をさせ、後からそこを切り捨てるのがよい。そのためには、たとえば上限値をはみ出した実測値(「1,890,000 → 100」と「1,280,000 → 100」)をデータから削除するんだ。テキストボックスからこの2行を消去して「fit model」ボタンをクリックすると、もっとましな結果が得られる。
また、僕が採用しているアルゴリズムは、すべてのデータポイントの重要度が等しいものとして比較しようとする。データのある部分がより重要だと思うのならば、その範囲の実測値を追加するといい。たとえば、最初のモデルでうまく予測できておらず、またユーザーの多くはおそらくこの範囲に当てはまるだろうと考えて、30%から65%の間にもう少し多くの実例が欲しいと考えるかもしれない。具体的には、「26,900 → 38%」「47,000 → 50%」というような行を追加することになるだろう。こうして新たな実測値を加えると、モデルはこの範囲のデータをより重視することになる。
また、たとえ「最適」モデルでなくても、見込みのありそうなほかのモデルも考えてみるべきだろう。たとえば、対数回帰モデルよりも、べき乗回帰モデルによる予測の方が好ましい場合があるかもしれない。ほかのモデルへのリンクをクリックして、モデルのグラフと残差を確かめよう。
僕らは社内で、こんな手法を使ってユーザーのページやドメイン、ブログを評価している。読者もこれらの手法を使って、データのふるまいをもっとよく理解することが可能だ。今度「もし因子Xを2倍にしたらどうなるだろうか」と誰かに言われたら、数多くの経験と数学モデルに基づいて、「一般的に、因子Xの重要度は対数的に減少する。グラフを使って表すと……」という具合に言ってやろう。
僕らがこれらのすばらしいモデルをどう活用するのか、例を1つ挙げておくね。
大学で学ぶ統計学はやはり大事だという事実から目を背けないこと!