【手数料の計算方法】入金額から逆算して求めるには？

代理店さんが絡んでる案件ですよね！ 代理店さんの販売手数料は15％だったはずです。先輩、たまには計算してください。

えー。仕方ないですねえ。電卓電卓…。ざっと293万円ですね。

えー。（255万円の15％を入金額に足したのはダメ～？ 納得いかない！）

300万円ってどうやって計算したの？ 教えてモリさーーん！

なんか超ライトな登場ですね。

さっそく本題なのですが、255万円の入金があったんです。この金額は、代理店さんがお客様への請求金額の15％を差し引いたあとなんですって。で、お客様への請求金額が知りたい！ という状況です。

255万円の15％を求めて、255万円に足したんですが、違うと先輩に言われました。

何に対してのですか。お客様への請求金額の、ですね。

たしかに。

それは任せてください。比べられる量 もとになる量 ＝割合 ですね。この連載の第1回で学びました！

それは第11回で学びました！「〇〇の△%」といったら、もとになる量に割合をかけるんでしたよね。

請求金額の15%なので、請求金額が「もとになる量」ですね。この金額がわからないんですよね。

𝒳×0.15=255万円ですか？

たしかに！ どうすればいいでしょうか。

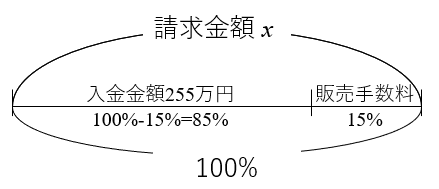
ということは、もとになる量の85%、つまり入金金額が255万円なので、式は𝒳×(1-0.15)=255万円 ですか？

モリさんも、たまには計算どうですか？

𝒳×0.85＝255万円、これを解くと 𝒳=255万円÷0.85=300万円！ 先輩の計算のと～りです！

やってみます。請求金額を𝒳とおいて、𝒳-𝒳×0.15=255万円。 ということは𝒳-0.15𝒳、よって0.85𝒳なので、あ、先ほどの計算と同じになりますね。 0.85𝒳=255万円、𝒳=300万円です。

分配法則？ 昔流行ったマーフィーの法則の仲間ですか？ 「洗車しはじめると雨が降る」とかでしたっけ。

カッコの外にある数字をカッコ内のそれぞれの数字にかけるんでしたっけ。

でも、最初の請求金額には何もかけていないですよね？

なるほど。だから、請求金額でまとめて、「請求金額×(1-0.15) 」とできるんですね。

ところで、担当することになったEC事業の目玉商品の販売価格が3150円なんです。この価格には、ショッピングカートの手数料5％が含まれているらしくて…。このとき、手数料を加える前の商品価格はどうやって求めればいいですか？

商品価格です。

手数料は商品価格の5％なので…。あれ、ちょっとわからなくなってきてしまった。3150×(1-0.05) ではない？

はい！ こんな感じでしょうか？

𝒳+（𝒳×0.05）=3150円 でしょうか？

さっき学んだこと、さっそく使ってみますね！ 𝒳×(1+0.05)=3150円 なので、1.05𝒳=3150
𝒳=3150÷1.05
𝒳=3000円

割合の基本ですよね。あと、今回のような場合のアドバイスはありませんか？

わかりました。ついつい、すぐに「〇〇の△%」の計算を使いたくなっちゃいますが、基本に立ち返ってよく考えることが大切なんですね。