比をヒントに、隠された数を見つけよう!

本屋さんに行くのが好きなんだよね。平積みになっている本を見ているだけで知らない世界が目に飛び込んできて、わくわくするんだ。

たしかに楽しいんですが、本屋さんに行くと、お手洗いに行きたくなるんですよね……。なんでだろう。

それ、「青木まりこ現象」っていうらしいよ。ところでさ、先日、本屋さんに行ったら、2人の姉妹が本を買ってたんだよ。
姉「私は6000円持ってきたわ」
妹「私は3400円持ってるよ」
姉「この本は2人とも欲しいのだから、割り勘にしましょう」
妹「いい考えだね」
姉「本を買ったあとの所持金の比、7:2になったわね」
妹「本当だ!本はいくらだったの?」
って会話をしててね。

先輩、そういうシチュエーション、夢か、算数の問題にしかないですよ。

夢だったのかな……。

そろそろこの連載も書籍として本屋さんに並ぶし、きっと本屋さんに行きたい願望が夢に出てきたんですよ!私は、主役ではないけれど、本は6/19に発売なので買ってください。

で、あの姉妹が買った本は4720円か……。

え、今どうやって求めたんですか? 夢? あ、コレ、夢じゃなくて算数の問題?

夢だけど、夢じゃなかったのかも。では、本の値段の求め方、考えといてね!昼寝してくる!

トトロ……! それより、昼寝の前に、教えてくださいー! せんぱーい!!
昔から、算数も数学も苦手なアユムは、希望が叶ってマーケティング部門に異動してきました。Web担で見るような「すごいマーケターになりたい!」と胸を躍らせていたが、配属後、理想と現実のギャップに苛まれることに。データ、数字、%、小数。うわぁーん、どうしたら、数字に強くなれるのでしょうか……。
そこに現れたのが、大人向け数学教室「大人塾」を運営し、数学苦手な社会人に対して指導をしているアジアゾウをこよなく愛するモリさん。

この記事を読むべき人:比の意味を理解したい方
この記事を読む必要がない人:相当算の問題を解ける方
この記事でわかること:比を使った問題の解き方
問題を解くカギ「相当算」とは?

この連載の書籍化、もうすぐですね! ワクワクします。

ええ、ワクワクドキドキですね。

ところで、姉が6000円、妹が3400円持っていて、本を購入するのに割り勘して同じ金額を出したら残金が7:2になった、という夢を先輩が見たらしいです。

夢!? 先輩、本屋さんに行きたい願望が強いのか、疲れているのでしょうか。ところで、その本の値段は、4720円ですね。

え、どうして? どうやって求めたのですか? 解説してください!

では、比の基本から学びましょうか。

はい!
算数のキホン! 「比」の考え方

比とはなんでしたっけ。

ひとは……城、人は石垣、人は堀……。

武田信玄かーい。「人」ではなくて、「比」です。比というのは、2つ以上の数の関係性をあらわしたものです。

関係……匂わせる感じですか。いますよね。そういう人。

人は匂えど、比は匂わせません。比は、a:bという形であらわし、a対(たい)bと読みます。数値を最大公約数で割って、もっとも簡単な整数の形であらわします。

対は「VS」の対ですか?巨人対阪神みたいな。

いえ、aとbは敵対しているわけではありません。a対bの「対」は、比べるという意味の「対」です。比べるといえば割合ですね。比も割合も、数量の関係をあらわす方法ですが、以下の違いがあります。
- 比は、複数の量をそのまま見比べて「aとbはこんな関係だよ」と示すもの。
- 割合 は、何か「もと」を決めて、それに対して「どれくらいか」を示すもの。

割合は、比べられる量/もとにする量ですよね。全体である「もとにする量」がちょっと偉そうだなって思ってたんですけど、比は対等なんですね。

割合をそんな風に思っていたんですね……。比のイメージはこんな感じです。同じ金額の入った袋がいくつかあるとします。このとき、姉妹の所持金の比が7:2であるとは、この袋をお姉さんが7袋、妹さんが2袋、それぞれ持っている状態です。ここでいう7とか2とかの単位は、袋1つにあたります。
小学生の解き方「差に注目!」

では、問題を解いてみましょう。方程式を使うと簡単に解けるんですが、ここは少し頭を柔らかくするために、まずは小学生のように𝒳を使わずに解きます。

文明の利器を使わない感じですか。小学生には負けたくない……どうやって解くんでしょう……。

図をかきます。数直線であらわしますね。

数直線って、左端を揃えるこんなんでしたっけ。
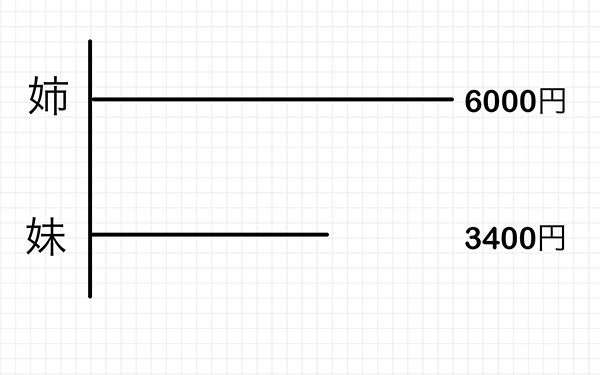

数直センだけに、センスいいですね。素晴らしいです。では、続けましょう。まずは、この数直線から、本の値段の部分を消しましょうか。

本の値段がわからないですよね。そんなナゾナゾみたいな……。

こうします。
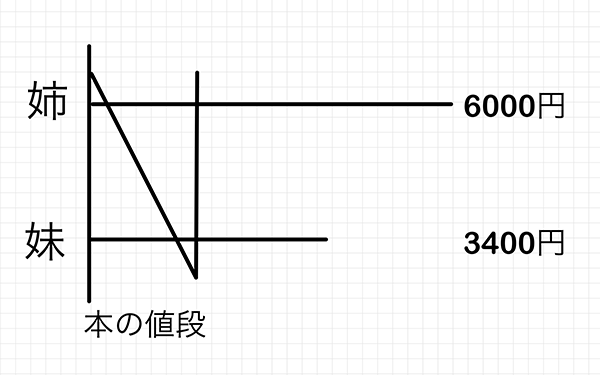

結構、適当に消しましたね。

人生そんな感じです。本の値段を引いて残った金額が7:2なので、以下のようにかきます。
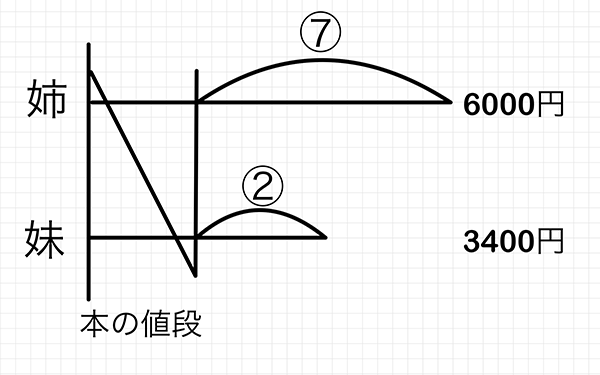

比の部分が丸数字なのはわざとですか?

はい、実際の数値が7なのではなく、比が7なので、区別しやすいように丸をつけて⑦としています。②も同じです。

はーい。

次は、変わらないものに注目します。姉と妹で本を買った後も変わらないものは何ですか。

2人の関係性? トトロのサツキとメイみたいに。でもよくよく考えると関係性は変わっているのかな? うーん、どうだったっけなあ……。

話が飛びすぎですね。戻りましょう。変わらないのは、2人の所持金の差です。

なるほど! たしかに、同じ金額を出して買ったのだから、姉と妹の所持金の差は変わらないですね! 姉と妹の差は6000-3400=2600円です。

そして、比は7:2。その差は?

⑦ - ② = ⑤です
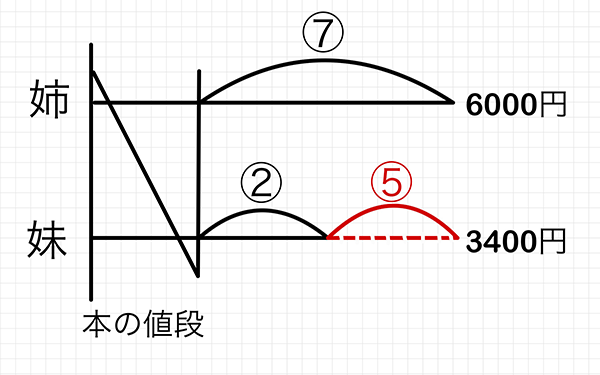

この⑤は比で、上の図の点線部分にあたりますね。つまり、比①を1袋と考えると、差は5袋分にあたるということです。ということは、1袋にいくら入ってます?

2600÷5=520 です。そうか、比①分にあたるのが520円なんですね。

ということは、妹さんの残金はいくらですか?

②なので、520×2=1040です。

妹さんは最初いくら持ってました?

3400円、ということは、本の値段は3400-1040=2360円! あれ?先輩の出した答えと違う……。

惜しい! 姉と割り勘したんですよね。ということは……。

なるほど、2360×2=4720円 が本の値段ですね。

大正解です! このように、比の単位である①がどれだけかを導く問題を「相当算」といいます。

相当面白いですね。あ、だから相当算というのか。

たぶん違います。
中学生の解き方「方程式を使用!」

今のは小学生の解き方で解いたんですよね。では、ちょっと大人になって中学生の解き方にも挑戦したいです。

では、大人として、𝒳を使った方程式で解きましょう。その前に、もう1つ、比の性質を覚えてほしいです。A:B=C:Dのとき、A×D=B×C となります。
たとえば、ここにとあるレシピがあります。1人分の調味料は、醤油大さじ2、みりん大さじ3です。3人分なら醤油大さじ6、みりん大さじ9。 このとき、醤油:みりん=2:3=6:9 とあらわせます。2×9=3×6となりますね。

性質ってなんか変な表現ですね。


ここで追い宣伝!

いわば文字のサブリミナル効果。では、それぞれ出した金額を𝒳円とおきましょう。2人の残金はどうあらわせますか?

最初の所持金は、姉が6000円、妹が3400円です。それぞれ𝒳円を支払っているので、残金は姉が6000-𝒳円、妹が3400-𝒳円です。

本の値段はどうあらわせますか?

2人の払った金額を合算するので、2𝒳です!

よっしゃー。𝒳が何をあらわすのか、求めるものが何なのかを確認するのは超重要です。では、比の形にあらわしましょう。姉の残金と妹の残金をA:B=C:Dという形であらわしてください。

6000-𝒳 :3400-𝒳 = 7:2となるのですか?

良い調子です。ではそれを計算しましょう。

(6000-𝒳)×2=(3400-𝒳)×7 ですか?

はい、それを展開してください。
(参考記事:四則演算の順番は? 掛け算や割り算、混乱しないルールを解説)

12000-2𝒳=23800-7𝒳

それを解くと?

5𝒳=11800、 𝒳=2360です。

ということは、本の値段は?

2360×2=4720円です! 小学生の解き方と同じ答えになりました!

算数・数学はこのように、複数の考え方で解けるから楽しいですよね。

ところで、自分、「どのようにあらわす」をずっと「どのように笑わす」と聞き間違えをしていて、数式を作らずにずっとギャグを考えてました……。

笑っていいのか笑っちゃダメなのか……さあ、アユムさん、ここでアユムさんが考えた珠玉のギャグで全読者さんを笑わせてください!

相当算の話から逸れすぎたら申し訳ないので、それでは来月~! さようならー!

え~! 思いつかなかっただけですよねー?
ポイント
- A:Bは数値を最大公約数で割って、もっとも簡単な整数の形であらわす。
- 「相当算」では、比の1にあたる量が具体的な数値でどれだけかを考える。
- 算数・数学は複数の考え方で解けるため、さまざまなアプローチを試すことが重要。
- 比の性質A:B=C:Dのとき、A×D=B×Cを覚える。
今日の問題をおさらい
Q1.姉が6000円、妹が3400円を持っていて、本を購入するために割り勘して同じ金額を出したら残金が7:2になった。本の値段はいくら?
【小学生の解き方】
6000-3400=2600…姉と妹の所持金の差
比の差は7-2=5
2600÷5=520 …比の単位に相当
妹の残金 520 ×2=1040
妹が本に支払った金額=妹の最初の所持金ー現在の残金=3400-1040=2360
本の値段 2360×2=4720(円)
【中学生の解き方】
姉妹がそれぞれ支払った金額を𝒳円とおく
6000-𝒳 :3400-𝒳=7:2
(6000-𝒳)×2=(3400-𝒳)×7
12000-2𝒳=23800-7𝒳
11800=5𝒳
𝒳=2360
本の値段 2360×2=4720(円)
答え:4720円
この連載が本になります!
おかげさまで300万PV以上を突破したWeb担の人気連載「算数基礎講座」が、全ページ書き下ろしでついに書籍化! その名も…
『コレ解ける? 数字がこわくなくなる おとな算数ゆるトレ』
こんな方におすすめ!
- 文系だけど算数を基礎から学び直したい
- 子どもに算数を教えたいけど、実は自分も自信がない
- 仕事で数字を使う場面が増え、苦手意識を克服したい
- 計算が得意な人に憧れる
- 手軽に論理的思考力を高めたい
……そんな大人のための算数トレーニング本です。今、発売に向けて最後の確認をしてます!
書名:コレ解ける? 数字がこわくなくなる おとな算数ゆるトレ
著者:モリマミコ(大人のための数学教室大人塾)
出版社:インプレス
価格:¥1,980 税込
発売予定日:2025年6月19日(木)

現在、Amazonで予約受付中です! ぜひチェックしてみてくださいね。