値上げ率の計算方法|元値はいくら? 何%上がった?
値上げ後の金額や値上率、元値を求める方法について詳しく説明します。「10%値上げ」といわれたときに、ピンとこない方に向けて、割合(パーセンテージ)の計算や値上げ幅、連続して値上げする場合の計算方法について、初心者でもわかりやすく解説!たとえば新価格から旧価格に改定した際などにぜひ参考にしてください!
2022年9月27日 7:00
昔から、算数も数学も苦手なアユムは、希望が叶ってマーケティング部門に異動してきました。Web担で見るような「すごいマーケターになりたい!」と胸を躍らせていたが、配属後、理想と現実のギャップに苛まれることに。データ、数字、%、小数。うわぁーん、どうしたら、数字に強くなれるのでしょうか……。
この記事を読むべき人:○%値上げといわれたときに、ピンとこない方
この記事を読む必要がない人:割合で表記された増加の意味を理解している方
この記事でわかること: 値上げ率の計算、割合であらわされた増加の計算方法10%値上げして165円。値上げ前はいくら?
 先輩
先輩どこもかしこも値上げだねー。原材料費もあがってるから仕方ないとはいえツライよね。

食品の値上げは、生活に直接関わってきますよね。ランチタイムもお財布が地味にダメージを受けてます。

私たちもそうだけど、ターゲットになる人たちの消費動向もチェックしていかなくちゃだね。
 アユム
アユムさすがですね! 先輩!
 先輩
先輩ところで、いつも事務所に置いてあるお菓子、10%値上げで165円になるってニュースやってたね、もともとは150円だったんだねー。

え、そうなんですか!?(何、それどうやって計算したの?)

そこに現れたのが、大人向け数学教室「大人塾」を運営し、数学苦手な社会人に対して指導をしているモリさん。

モリさん! 値上げの計算を教えてください!

なんですか、藪から棒に。何か起きたんですか?
 アユム
アユム10%の値上げで165円になった商品のもとの値段をすぐ計算できるようになりたいです!

なるほど。これも割合の問題ですね。
500円→550円、値上げ率はいくら?
 モリ
モリやりたいことに取り掛かるためには、値上げの構造を把握しましょう。値上げ前の値段に、値上げ分の金額が足されて、値上げ後の値段になりますね。

 アユム
アユムこれはわかります。値上げ分が乗っかるんですよね。

では、たとえば500円の商品Aが550円に値上げしたとき、または1000円の商品Bが1080円に値上げしたとき、それぞれの値上げ分の金額はいくらですか?

500円の商品Aは550円なので、値上げした金額は50円ですね。同じように、1000円の商品Bは80円だけ値上げしたと。

それでは、どちらの方が値上げ率が高いでしょう?

値上がりした金額はBの方が高いけど、「率」だから……。
前回のお話だと、割合は「もとになる量」と「比べられる量」で求めるんでしたね。どっちがどっちだろう……。
 モリ
モリ「もとの値段に対する値上げ金額」なので……。
 アユム
アユムもとになるのは、値上げ前の値段ですね!
 モリ
モリその通り!「○○に対して」ということは「○○を基準として」と同じ意味です。つまり、値上げ前の値段が、もとになる量です。

ということは、比べられるのは、値上げした金額分ということか。

すばらしい!つまり、下のようにあらわせますね。
比べられる量 もとになる量=値上げした分 もとの値段

なるほど! もとの値段に対して、値上げした分がどれだけにあたるか、ということですね。
 モリ
モリそうです。割合にしたことで、もとの値段が違っても、比較することができるんですね。それでは、商品A、商品Bについてみてみましょう。

商品Aは、50 500=0.1
小数点を2個、右にずらして……。10%ですね。
商品Bは、80 1000=0.08
だから8%ですね!
つまり、商品Aの方が値上げ率が高いですね。
そうか、前回は「100人の村とすると」だったけど、今回は「100円とすると」なんですね!

はい!バッチシですね。
10%値上げして550円になった商品のもとの値段はいくら?

もとの値段に対しての値上げ分の金額を割合で求める方法は、わかりました。では、値上げ後の値段からもとの値段をシュッ! と計算したいです。
 モリ
モリシュッ! いいですね。それでは、さきほどの図に戻って考えましょう。
さきほど、値上げ前の値段が「もとになる量」であるという話をしましたね。
例えば、商品Aは値上げ前が500円で、50円の値上げをしたので、下のようにあらわせます。
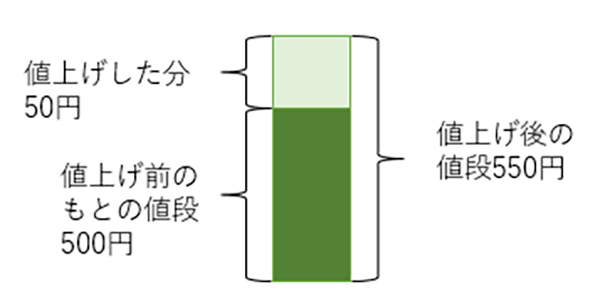

はい、そうですね。

500円を100%としたときに値上げの50円が10%にあたります。
ということは、値上げ後の値段は、値上げ前の値段の何%になりますか。

もとの値段100%に10%足すので、110%になりますね。
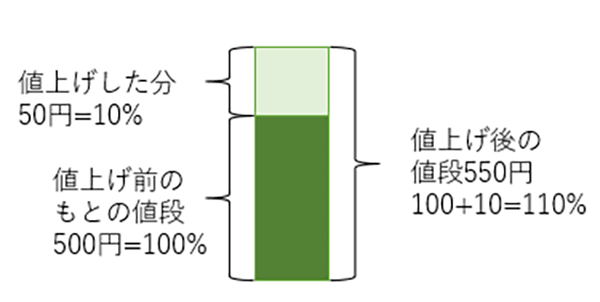

ですです。
比べられる量 もとになる量=割合
この式を変形すると「もとになる量×割合=比べられる量」という式になりましたね。
たとえば、値上げ前の値段がわからないとき、xとおくと、x× 110%=550円となります。
110%は、小数に直すと1.1なので、
x=550÷1.1を計算してx=500(円)となり、もとの値段がわかりますね!

ということは、先輩が計算した10%値上げして165円になった商品は……
165÷1.1=150
で求められるってことなんですね。

その通りです!
1000円の商品を15%、10%と連続して値上げするといくら?

ところで、素朴な疑問なんですが。

はい、どうぞ。

ある商品が昨年の冬に15%値上げして、この夏にまた10%値上げしたとします。昨年の値上げ前よりも15+10=25%だけ値上げした、ということになるんでしょうか?

いい質問ですね。
最初の値上げ前の値段を1000円として考えてみましょう。冬の値上げでいくらになりますか?

15%の値上げで、もとの値段を100%とするので、100+15=115(%)になる、ということですよね。なので、1000円×1.15=1150円です。

だとすると、夏の値上げ前の値段は1150円ですね。それをもとになる量、つまり「100%」として次のステップへ進みます。

え、さっきまで115%だったのが100%になるんですか? ちょっと混乱しちゃう。

ここは、みなさんが混乱しやすいポイントです。割合の「もとになる量」は、今、この時点で、何をもとにしているか、の数値です。なので今回の場合は、夏前の時点の1150円という値段が「もとになる量」なのです。

そうか、何をもとにするかを自分で決めているから、今、この時点で、もとになるのは1150円なんですね。で、これがもとなので100%にあたると。ふむふむ。
 モリ
モリはい、それでは夏の値上げの計算にいきましょうか。
 アユム
アユムいろいろ気が重いなあ。夏は10%の値上げなので、もとの値段を100%とすると、110%になるということですよね。
つまり、1150円×1.1=1265円。
昨年の冬の値上げ前から265円も値上げしたんですねえ……。
 モリ
モリさて、では疑問について、あらためて考えてみましょうか。昨年の冬の値上げ前は1000円でしたよね。さて、どれだけ値上げしましたか?

値上げしたのは265円、この場合、比較しているのは昨年の冬の値上げ前の値段だから、もとになる量は1000円。
比べられる量 もとになる量=値上げした分 元の値段=265円 1000円
265÷1000=0.265
これを%に直すには、小数点を2つ右に動かせばいいので、26.5!
値上げ率は、26.5%ってことですね。

はい、正解です。ちなみに分数であらわす場合、分母を100にすれば、その分子が%になります。
26.5 100

ちょっと計算が速くできますね。

では、どうでしょうか。アユムさんの質問にあった「25%値上げ」になっていますか?

なっていないですね。26.5%ですもんね。25%より値が大きいですね。
 モリ
モリはい、今回のように連続して値上げするときは、単純に足すよりも、もとになる量が大きくなったぶん、変化分が大きくなりますね。

なるほど。ちなみに、段階を踏まず、一気に計算するにはどうすればいいですか?

(冬の値上げ前の値段)×1.15×1.1=(冬の値上げ前の値段)×1.265 で計算できますよ。

あ! さっきの26.5の値ですね! でも、1.265ってなってますね。この「1」ってなんでしたっけ?

これは本体の価格。というか、冬の値上げ前の値段をあらわしています。昔、「1とおくと」と習いませんでしたか?

習いましたねー。なにが1なのかよくわからなくて、あの辺から算数に挫折した気が……。

あれは、1、つまり100%、もとにしている量そのものです。

 アユム
アユムそういう意味だったんですね。つまり、値上げ分が26.5%のとき、値上げ後の値段を求めるには、もとの値段を足した126.5%になる、ということですね。
 モリ
モリはい、なので、
もとの値段+もとの値段に対する値上げ分
=1000+1000×0.265
でも求められます。

なるほどー。「1とおくと」って、そういう意味だったんですね。
 モリ
モリ「割合の増加(増加率)」といいます。今後は、この計算はできそうですね!
 アユム
アユムはいっ、シュッと求められそうです!

よかったです! では、また来月!
今日のおさらい
増加後の量を求める。
もとになる量×(1+増加した割合)=増加後の量
もとの量を求める。
増加後の量÷(1+増加した割合)=もとの量
連続して増加する場合の増加後の量を求める。
もとになる量×(1+増加した割合)×(1+増加した割合)=増加後の量
今日の問題をおさらい
Q1.10%値上げして165円。値上げ前はいくら?
もとの値段をxとおくと、x×1.1=165
165÷1.1=150
答え:150円
Q2.500円→550円、値上げ率はいくら?
値上げした分は、550-500=50
「比べられる量 もとになる量」で求められるので、
50 500=10%
答え:10%
Q3.1000円の商品を15%、10%と連続して値上げするといくら?
1000×(1+0.15)×(1+0.1)=1265
答え:1265円