GoogleのPageRank(Googleツールバーが表示する小さな緑のインジケータではなく生の値)の裏にある「ランダムサーファー」について知っている検索マーケティング担当者は多い。Google自身の表現を借りれば、以下のようになる。
PageRankは、ユーザーの挙動を表した1つのモデルと考えることができる。たとえば、無作為にウェブページを訪問して片っ端からリンクをクリックし、決して「戻る」ボタンをクリックせず、最終的にはそこに飽きて別のページで同じことを繰り返す「ランダムサーファー」がいると仮定する。そうしたランダムサーファーがページを訪問する可能性を示すのがPageRankである。
別の言い方をすれば、あるページに対するリンクが多ければ多いほど、そのページはたくさんの「票」を獲得し、その結果PageRankも高くなるというわけだ。もう少し深く掘り下げて言うと、票の重さはリンク元の各ページが持つPageRankによって決まり、これが参照先ページにあるリンクの量に加わるということだ。
だが、SEOmozのシー・フィッシュキンが鋭く指摘している通り、このPageRankの初期モデルには、いくつか深刻な限界があった。研究論文(PDFファイル)に記されている最終的な方程式では、この記事を読めばわかるが、その限界を修正する調整を施している。この記事は相当数学的な話になるので、その点を警告しておくよ。さあ、がんばって!
初期のPageRankにおける限界
基本モデルに存在した限界は、ここに示す通りだが、すでに十分な論拠がある。
- ランクシンク(Rank Sink)
あるページに外向きのリンクがないとき、そこにランクシンクが発生する。言うなれば、PageRankを吸い込むトラップのようなものだ。PageRankは、値が安定するまで価値の計算を繰り返し実行する(再帰計算)が、ランクシンクはその値を共有せず独占する。下図でいうと、「Page C」がランクシンクだ。

- ホーディング(PageRankため込み)
ランクシンクの延長線上にあるのがこれ。互いの間だけでリンクし合っているページ群もPageRankを独占する。Wikipediaが好例で、外部サイトにリンクするときにはすべてnofollow属性を使っている。下図では、「Page D」「Page E」「Page F」がPageRankのホーディングを行っている。

- 循環参照
ある2ページが、互いの間でだけリンクし合って、他所には一切リンクしていない状態を指す。アルゴリズムがエンドレスのループに閉じ込められるため、再帰計算のプロセスが収束することはない。
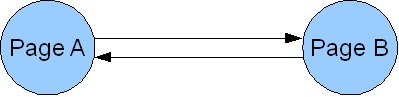
ただ幸いなことに、これらの問題点は早い段階で確認され、2つの重要な調整を施すことで改善された。
調整その1:確率論の採用
PageRankの方程式には、非常に冗長な総和計算のプロセスが含まれている。ウェブのハイパーリンク構造は、行列式(Excelに似たもの)でモデル化することが可能だ。これを行列Hと呼ぶことにする。
行列式を使用すると、これらの総和計算をより単純なベクトル・行列の掛け算に変換できる。つまり、それだけ計算時間を短縮できるということだ。また行列式では、行列代数とマルコフ連鎖モデル(PDFファイル)の理論を応用する。行列Hでは、行と列がページを表し、交差したところの値(0または1)がページ間のリンクの有無を示す。ただしここでは、リンクの存在を示すのに1ではなく1/xを使う。xは各行に存在する0以外の要素の数だ。この手法は、0以外の値を確率に置き換え、行に関する準確率論的行列を作成するものだ。つまり基本的には、各行の値を合算していくと、合計が1になる部分と0になる部分が出てくることを意味する。合計が0になる要因は、ノードのぶら下がり現象、すなわちランクシンクの存在だ。行確率論的な行列では、すべての行で合計の最大値は1になる。
前述の問題に加え、行列に手を加えなかった場合には、何度計算を行っても値が収束するとは限らない。これらの問題を修正するために導入したのが、この調整その1だ。この調整では、すべて0の行(ノードのぶら下がり現象つまりランクシンクの起きている行)を1/n eT(eTはすべて1の行ベクトル)で置き換え、確率論に沿った行列を作成する。この修正した行列を行列Sと呼ぶ。この行列が、マルコフ連鎖に対する推移確率行列だ。
直観的に、この調整が外部にリンクを張ろうとしないページに対応するもので、アルゴリズムが行き詰まらないよう、修正モデルで自動的に目に見えないリンクを作成しているのがわかるだろう。「ランダムサーファー」がぶら下がりノードに入っても、その人はどのページにでも無作為にハイパーリンクできるという状態を作り出す。
調整その2:原初性調整
さてランクシンクに起因する問題を解決するほかにも、すべてのページのPageRank値がすばやく(できるだけ少ない再帰計算で)求められる方が望ましい。
幸いなことに、マルコフ行列にべき乗法を適用すれば、行列が確率論を適用したものであり、それ以上単純化できない非周期的なものならば、「定常ベクトル」と呼ばれる固有のポジティブなベクトルに収束する。今ここで論じているケースでは、これがPageRankベクトルになる(非周期性と一定以上の単純化不能は、原初性を示している)。
直観的に原初性調整は、ウェブのハイパーリンク構造を辿りながらときどき退屈し、無作為にリンクを辿るのやめて、ブラウザのナビゲーションバーに新しいURLを入力し、そこからまたネットサーフィンを続けるランダムサーファーを考慮したものということがわかる。これは、無作為にリンクを辿る時間と、新しいURLに「テレポート」する時間との比率を表す。
これを数学的にモデル化するため、ここで新しいファクターαを導入する。これは0と1の間のスカラーだ。論文を記したラリー・ペイジとサーゲイ・ブリンは最初、このαを0.85と定義した。つまり、ウェブサーファーは全時間の85%を無作為にリンクを辿って過ごし、残りの15%の時間はアドレスバーに新しいURLを入力すると仮定したことになる。
この調整から新しい行列が生まれた。これを行列Gと呼ぶ。Google行列(マトリックス)の誕生だ。行列Gは次のように表すことができる。
または
G = α S + (1 - α) E
Eは、アドレスバーに新しいURLを入力する「テレポート」の行列だ。
eTはすべて1の行ベクトルだったのを覚えているだろうか。
テレポート行列E = 1/n eeTが一律であることから、テレポートは無作為に行われる。これはつまり、ランダムサーファーはテレポートする際に、あらゆるページに等しい確率で移動することを意味する。
結論
ランダムサーファーがとるテレポート行動と、ランクシンクを相殺するために導入した見えないリンクのおかげで、サイトが外部にリンクしていない状態や、PageRankホーディングの効果について、あまり心配せずに済む。そうした状況はすべて1998年に観測され解決済みだ。
今では彼らの使っているPageRankのアルゴリズムは、はるかに進んでいると僕は確信している。たとえば、みんなもよく知っているとおり、Googleは1か月に1度インデックスを更新する(月に1回というのは、ウェブ上にあるすべてのページのPageRankを計算するには膨大な時間がかかるため、という理由もある)。しかもインデックスの更新は、追加的に行われることもわかっている。たぶんGoogleは、部分的にまたは増加分だけPageRankを計算する方法を見つけ出したのだろう。
ここまでよく頑張って読み通し、理解しようと努めてくれたね。僕もこれを調べて書くのは大変だったけど、君の頭は今、僕の頭と同じくらい疲れていると思うよ(^-^)。できるだけやさしい言葉でこれを説明しようとしたけど、残念ながら、細かな部分を完全に理解するには、数学を持ち出さないわけにはいかないからね。
参考資料(すべて英語)
- マルコフ連鎖モデル(PDFファイル)
- PageRank研究論文(PDFファイル)
- PageRankのより深い内面:PageRank算定原理論文(PDFファイル)
- Google's PageRank and Beyond: The Science of Search Engine Rankings(書籍)