組み合わせは何通り? 5種類から2種類選ぶ時の計算方法・余事象の使い方
5種類から2種類選ぶ時は5C2? イベント来場者に景品をプレゼントする事例をもとに「場合の数」における「組み合わせ」や「余事象」について解説します。積の法則や和の法則も算数が苦手な方でもわかりやすく事例と一緒に学んでいきましょう!
2023年2月28日 7:00
昔から、算数も数学も苦手なアユムは、希望が叶ってマーケティング部門に異動してきました。Web担で見るような「すごいマーケターになりたい!」と胸を躍らせていたが、配属後、理想と現実のギャップに苛まれることに。データ、数字、%、小数。うわぁーん、どうしたら、数字に強くなれるのでしょうか……。
この記事を読むべき人:組み合わせをすぐに算出できない方
この記事を読む必要がない人:順列・組み合わせの基本をすぐに算出できる方
この記事でわかること:組み合わせ、積の法則、和の法則、余事象
5種類のアクリルスタンドのうち2種類もらえるとき、組み合わせは何通り?

今度のイベントで、イベントキャラクターのアクリルスタンドを5種類用意して来場者にプレゼントします。1人につき2種類もらえるようにする予定です。

なるほど、アクスタいいんじゃないかな。2種類もらえるということは10通りのもらい方があるということか。これくらいバリエーションがあるとおもしろそうだね。

10通りですか!
(なに!? どうやって数えたの? 前回、覚えた順列の計算だと10通りにならないし、何が違うんだ?)

アクスタの写真をSNSとかにアップしてもらうキャンペーンと組み合わせてもいいかも。そういう撮影できそうな場所も用意して……。

(10通り……どうやって?)

あれアユムさん、話し聞いている??

そこに現れたのが、大人向け数学教室「大人塾」を運営し、数学苦手な社会人に対して指導をしているモリさん。

モリさん! 先輩が、よくわからない方法で数えました!

アユムさんの質問もよくわからないですが、一体何が起きましたか。

5種類のアクスタから2種類選ぶのですが、その組み合わせのパターン数をささっと数えられるようになりたいです。

なるほど。では早速、数えていきましょう。
まずは樹形図を書こう

前回、順列を学びましたね。順列は順番があるものの場合の数を計算する方法でした。

はい、バッチリ覚えてます。

今回のアクスタは、順番はありますか?

いえ、順番は関係ないです。

それでは、アクスタをA、B、C、D、Eとおきましょうか。まず、樹形図をかきましょう。

はい! Aをもらった場合、残りはB、C、D、E の4通りですね! ということは、5×4=20通りではありませんか? あれ? 先輩の出した答えのちょうど2倍になっちゃってますね。


整理してみましょう。それでは、今の考えで樹形図の続きをかいてみましょうか。

では、Bをもらった場合についてかいてみますね。
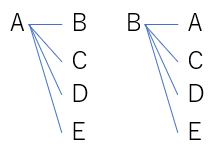

A、Bの組み合わせ、ダブってませんか?

確かに! これは、同じ組み合わせですね。

ということは、ダブりなくC、Dと樹形図にするとこんな感じですね。あ、先輩の言う通り、全部で10通り!
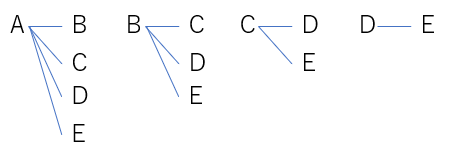

はい、その通りです!
組み合わせの公式を使って求めてみよう

これをさささーと計算できるようになりたいです。

そういうときは、公式を使いましょうか。
まず、組み合わせの公式は、
𝑛C𝑟とし、 𝑛𝑃𝑟 𝑟! で求めます。
これは、𝑛個から𝑟個の個数を選ぶということです。
5種類のアクスタから2種類もらう場合、5C2とあらわします。

Cは何の略ですか?

コンビネーション(combination)、日本語に訳すと「組み合わせ」、そのまんまですね。

どういう計算をするんですか?

ざっくりいうと、分子は、𝑛から大きい順に数字を𝑟個かける。この例では、5から大きい順に数字を2個かけます(5×4)。これが𝑛𝑃𝑟です。
分母は、𝑟から1までの数字を掛け合わせる。この例では、2から大きい順に数字を2個かけています(2×1)。これが階乗です。
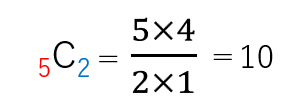

どうしてこうなるんですか?

5つから順番に2つをとる場合は、順列の公式を使って5𝑃2。よって5×4=20です。

樹形図にかくとこんな感じですよね。


2つのものの並び方は、2通りですね。例えば、ABの並び方は、ABかBAしかありませんね。これを「2!(2の階乗)といいます」。

「!」ビックリするんですか?

いえ、これは「階乗(かいじょう)」といって、𝑟! のとき𝑟の数から大きい順に1までかけていくことを表しています。

ビックリして1まで掛け算しながら走り抜けてしまったイメージですね!

(? まあいいか)公式にあるように、順列の計算で出る場合の数を、選ぶ個数(𝑟)の階乗で割ることで、組み合わせのパターンの計算になるのです。
なので今回の場合、順列で5つから2つ取り出した5𝑃2を、2つの階乗で割ります。
5C2= 5𝑃2 2! となり、計算すると 5×4 2×1 =10となります。

なんかクラクラしてきました。

別の問題で、この計算を練習しましょうか。イベントの設営にはアユムさんの同期7人から3人お手伝いが必要と聞きましたが、選び方は何通りですか?

これは順番がないので組み合わせの問題ですね?

その通りです! アユムさんとほかの2人が何番目に選ばれようと同じ人が集まれば同じグループとなりますよね。

となると、𝑛C𝑟の公式にあてはめて、7人から3人の組み合わせなので7C3になって、 7×6×5 3×2×1 = 35通りですね。

正解です!
積の法則を使ってみよう

設営の話で思い出したのですが、同期7人のうち、力仕事が好きな人が3人いて、残りの4人は几帳面なんですよ。この2つの性質をうまくミックスして設営にあたりたいです。

適材適所ということですね。

そこで、力仕事が好きな1人、几帳面な2人をあわせた3人のチームを組んだらいいのではないかと思います。これって何通りになるか、どうやって求めればいいですか?

それでは、まず、力仕事が好きな1人を選ぶのは、何通りですか?

3人から1人選ぶので3C1で、3通りですね。

几帳面な2人を選ぶのは?

4人から2人選ぶので4C2で、6通りですね。

力仕事が好きな3人をA、B、Cとしましょうか。
さて、樹形図をかきましょう!

ガッテン。こんなのどうでしょう? 力仕事が好きなAさんと紐づくグループは6通りです。
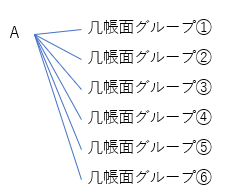

よいですね。つまり、力仕事好きな人は3人いるので…?

なるほど、3×6=18通りですね!

正解です。異なるグループごとに選んで、それをパターンごとに組み合わせるときは掛け算をします。これを「積の法則」といいます。

あ、机とか椅子とか設営するから、席の法則ですか?

違います。その席ではありません。掛け算のことを積というので、積の法則です。
余事象という考え方を知ろう

設営って力仕事に見えるんですが、几帳面さも欠かせないんですよね。3人を選ぶときに、少なくとも1人は几帳面な人を入れる場合は何通りですか?

几帳面な人、重要ですね。その場合は「余事象」という考え方を使います。先に言っておきますが、余りとなる事象の話であって、ゾウさんの話ではないですよ。

そういえば、森さんは大のアジアゾウ好きでしたね。

はい! 象とかゾウという文字が出てくるだけでウキウキします。で、余事象(よじしょう)の話でしたね。余事象というのは、そのできごとが起こらない事象のことです。

むむ?

例えば、少なくとも1人は几帳面な人を入れるということは、力仕事が好きな人だけのグループではないようにしたいということですよね?

そうですね。だから、全員が几帳面でもいいんです。

では、几帳面な人が入っているパターンはどんな感じになりますか?

「几几几」「几几力」「几力力」のパターンがありますね。

そうですね、でもこの3つをすべて数えるには3回組み合わせの計算が必要です(これはあとでやります)。

なるほど。

上のパターンに含まれないのは「力力力」のパターンだけということに気づきますか?

確かに。

ということは、すべての組み合わせの数から「力力力」のパターンを引けば「几帳面が少なくとも1人は入る」場合になりますね?

確かに!!!

では、やってみましょう。全部の組み合わせは何通りですか?

7人から3人選ぶので7C3で35通りです。

力仕事が好きな人だけの組み合わせは何通りですか?

3人から3人選ぶので3C3で、1通りですね。

つまり……

35-1=34通りですか!?

大正解!
このように、全体の事象(場合の数)の数から起こらない事象(
和の法則を使ってみよう

では、余事象の計算が本当に正しいか検証しましょう。先ほど、グループのメンバーは「几几几」「几几力」「几力力」のパターンがあるという話になりましたね。
それぞれのパターンにおいて何通りあるかを確かめましょう。
まず、「几几几」のパターンです。これは、几帳面さんを3人選んでるんですね。

つまり、4人から3人選ぶ、4C3で4通りですね。

次に「几几力」はどうでしょう。

几帳面さんは4人から2人選んで、力仕事好きさんは3人から1人選んで、積の法則ですね(キラーン)。

いいですね。その通りです。

4C2は6通り、3C1は3通り、6×3=18通りです。

最後に、几帳面さん1人、力仕事好きさん2人ですね。

几帳面さんは4C1で4通り、力仕事好きさんは3C2で3通り、積の法則で4×3=12通りですね。

コホン、コホン。あってます。

咳(せき)……。

そう、積(せき)は掛け算です。でも、ここでは足します。
「几几几」4通り、「几几力」18通り、「几力力」12通りを足すと何通りですか?

4+18+12=34通り! 先ほどの余事象で計算したときと同じ数になりました!

このように複数のパターンの場合の数を求めるときは、それぞれのパターンの場合の数を出して足します。これが「和の法則」です。

わー。

わー(和)は、足し算ですね。
ここで大切なことは、パターンをきちんとかき出すことです。漏れなくダブりなくかき出すのは、すべての基本。情報をしっかり整理して条件をかきだせるようにしましょう。

すべてのパターン数や条件ごとのパターン数を手軽に導けると、考えをまとめる際の武器になりそうです。

はい。何かを選ぶというとき、順列、組み合わせの考え方があることを頭に入れておくと、意外なパターンの見落としなども減りますよ。
ポイント
- 組み合わせとは、順番がないものを選ぶ方法。異なる𝑛個のものから異なる𝑟個のものを組み合わせるという意味
- 公式だと「𝑛C𝑟」。計算方法は、「𝑛C𝑟= 𝑛𝑃𝑟 𝑟! 」
- 続けて組み合わせを考えるときは、それぞれの場合の数をかける積の法則
- 違うパターンを考えるときは、それぞれの場合の数を足す和の法則
- 特定の事象が起こらないことを考えるときは、余事象
- 樹形図とは、木の枝のように場合分けをあらわしたもの
今日の問題をおさらい
Q1. 5種類のアクリススタンドから2種類を選ぶ組み合わせは何通り?
5C2= 5×4 2×1 =10
答え:10通り
Q2. 7人から3人選んで、会場設営の手伝いをする場合、選び方は何通り?
7C3= 7×6×5 3×2×1 =35
答え:35通り
Q3. 7人のうち、力仕事が好きな人が3人、残りの4人は几帳面。力仕事好き1人、几帳面2人の3人でチームを組むとき、選び方は何通り?
3C1 × 4C2= 3 1 × 4×3 2×1 =18
答え:18通り
Q4. 選んだ3人のうち、少なくとも一人は几帳面な人が含まれるようにするのは何通り
余事象で求める場合:
7C3 - 3C3=34
和の法則で求める場合:
全員几帳面:4C3=4
1人几帳面:3C2×4C1=12
2人几帳面:3C1×4C2=18
4+12+18=34
答え:34通り