【場合の数】何通りの計算方法は？ 順列の公式や樹形図をやさしく解説

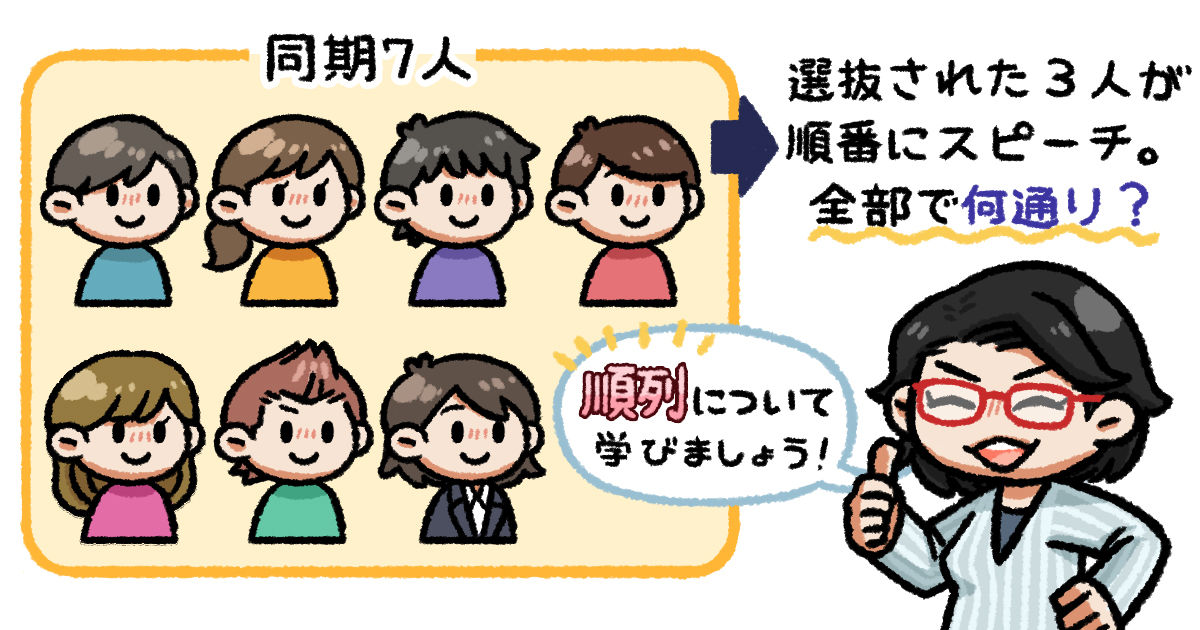
次の学生向けの企業説明会で、アユムさんの同期から3人に会社の先輩としてのスピーチをお願いしたいんだけど。

歌う必要ないよ。ところで、アユムさんの同期は何人だっけ？

ということは、スピーチの順番まで考えると、全部で210通りだね。

何をそんなに早く数えたいんですか。

なるほど、順列の問題ですね。

違います。純烈ではありません。漢字も違います。「順番に列に並ぶ」の「順列」です。

順列の考え方を理解するために、人数を少なくして考えましょうか。

ひっぱりますね（笑）。それでは、その4人の並び順について考えてみましょう。仮にその4人をA、B、C、Dとしましょう。まず、「A」をかいてください。

それでは、横に枝をかきます。
Aの次に来るのはBかCかDですね。枝を3本かき、その先に、B、C、Dとかいてください。

Bの後ろにくるのは、CかDですね。同様に、C、Dの後に並ぶのは残りの2人ですね。それをあらわしてみましょう。

これでAさんが最初に並んだ場合、何通りになりますか？

ということは、Bさん、Cさん、Dさん、それぞれが1番のときはすべてで何通りになりますか？

このように枝分かれした図をかきながら、並び順を数え上げる方法を樹形図をかくといいます。
かくときのポイントは

• 条件を漏れなく順番に
• 考えすぎずに、端から丁寧に

です。

わかりました。早く数えあげるには、目を鍛えるか、公式を覚えるかがいいでしょう。ここでは公式を使って解く方法を覚えます。ただし、公式を覚える前にもう一度樹形図を確認しましょう。

それぞれ、何本に枝分かれしたのかを確認しましょう。

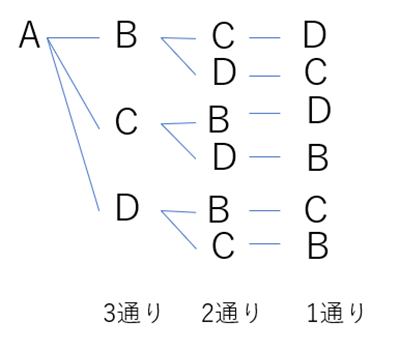
Aから出ている枝は、B、C、Dの3通りですね。つぎに、3番目にいるのは、2通りです。最後に並ぶのは、残り1人しかいないから1通りですね。

1番目は、A、B、C、Ｄの4候補いるので、4通りです。

それぞれ次の順番に並ぶ候補は、残りの人の分あるということです。ということは、掛け算をすればいいのです。この場合だと、4×3×2×1=24（通り）です。

このように、順位や役職など順番があるもの（A→BとB→Aの違いに意味があるもの）を順列といいます。順列の計算方法は「最初の候補数 × 次の候補数 ×……」と次々とかけていきます。

公式では 𝑛𝑃𝑟 と表します。異なる𝑛個のものから異なる𝑟個のものを順に取り出すという意味です。この場合は 4𝑃4=4×3×2×1=24 です。

英語の “permutation” （パーミュテーション）の略ですね。日本語では「順列、整列、並べ替え」など、並ぶ順番に意味がある言葉です。

4人から2人を順に並べるので、4𝑃2となり、4×3=12通りになります。

それでは解いてみましょうか。再確認ですが、話す人たちの順番を決める必要がありますよね？

それならば順列ですね。全部で何人なんでしたっけ？

何人話すんでしたっけ？

公式にあてはめると…？

先輩が猛烈に数えるのが早いのでなければそうだと思います。

公式を覚えると、解くのは速くなりますが、樹形図もしっかりかけるようにしておきましょう。

いいですね！イメージをきちんと持てれば、公式を忘れたとしても計算できますよ。

例えば洋服を決めるときとかにも使えますよ。シャツを5枚、ズボンを3枚持っているときの組み合わせは…？

そういうときこそ、樹形図に戻りましょう。ズボンをA、B、C、シャツをP、Q、R、S、Tとして、樹形図をかいてみましょう

となると、ズボンとシャツの組み合わせは…？

それでは次の問題です。部内で一人コントをするとしましょう。

10人の部署で2回一人コントをするイベントを催します。同じ人が2回舞台に立ってもいいとすると、その順番は何通りですか？

そういうことです。樹形図にしてみましょうか。

その通りです。〇通りと聞かれた場合は、質問の内容をしっかり理解しましょう。

はい、この場合の数は、確率をだすときにも必須の考え方なので、しっかり理解しておきましょう。