【計算できる?】鍵穴3つ、鍵12本、3つの鍵穴に正しい鍵が同時にセットされないと開かない。最大試行回数は?
算数が苦手な、新人マーケターのアユム。今回は大人が意外と忘れている「順列」「組み合わせ」の計算について解説します。
2024年11月27日 7:00
3つの鍵穴に正しい鍵が同時にセットされないと扉は開きません。最大試行回数は?

アユムさーん、ちょっと手伝って。

どうしたんですか? 鍵をじゃらじゃらさせて…。新しいファッションにハマってるんですか?


ハマってるのは、鍵のマッチング……。このキャビネットの扉には番号の付いた3つの鍵穴があって、それぞれの鍵穴に対応する正しい鍵をすべてセットしないと開かないんだ。この12個の鍵を片っ端から試すしかなくて...。



すっごい大変な扉ですね…。鍵は、全部でいくつあるんですか?

鍵は12個あるんだよ…。ってことは、最悪の場合、1320回も試さなくちゃいけないんだ…。

えっ。その数字、どうやって求めたんですか? 多すぎじゃないですか?

5回試しただけで飽きてきた…。いい眠気覚ましだと思ったけど大後悔だ。大後悔時代だ!

先輩、落ち着いて! 大変そうですね。えーと、自分は、その計算方法を考えるために、席に戻りますね!(ダッシュ!!)

ちょっと待ってー…。アユムさん、見捨てるの!?
昔から、算数も数学も苦手なアユムは、希望が叶ってマーケティング部門に異動してきました。Web担で見るような「すごいマーケターになりたい!」と胸を躍らせていたが、配属後、理想と現実のギャップに苛まれることに。データ、数字、%、小数。うわぁーん、どうしたら、数字に強くなれるのでしょうか……。
そこに現れたのが、大人向け数学教室「大人塾」を運営し、数学苦手な社会人に対して指導をしているアジアゾウをこよなく愛するモリさん。

この記事を読むべき人:順列、組み合わせを理解したい方
この記事を読む必要がない人:順列、組み合わせの問題を解ける方
この記事でわかること:順列と組み合わせの違い、解き方
最大試行回数の1320回はどうやって求めたの?

手伝えなくて、残念だなぁ。(ああ、逃げられてよかった、よかった。)

あらアユムさん、ニコニコしてますが、いいことでもありましたか?

先輩がキャビネットの鍵合わせをしていて、作業を自分に押し付けようとしてきたんです。無事に回避できたので、ついつい本音が顔に出てしまったようです。

あらまあ。どういう状況ですか?

キャビネットに3つ鍵穴があって、全部マッチしないと開かないんですって。そして、候補となる鍵が12個もあるんです。

ということは、最大1320回試す必要があるんですね…。アユムさん、逃げて正解ですね。

その数字、どうやって出したんですか?

これは順列の問題ですね。解いてみましょう。まず、状況整理です。番号のついた鍵穴が3つ、鍵が12個あります。3つの鍵穴にそれぞれ対応する正しい鍵をすべてセットしないと扉は開きません。では、1つ目の鍵穴にセットする鍵の選び方は、何通りありますか。

12通りです。

では、1つ目の鍵穴にセットする鍵を決めたとき、2つ目の鍵穴にセットする鍵の選び方は全部で何通りありますか。

鍵は12個なのでやっぱり12通りですか。

いいえ、1個目の鍵穴で1つ使ったので、残りは...。

11通りですね!

ということは、最後の鍵穴は?

10通りです!

そう。だから12×11×10で1320回になるんです。
順列Pの考え方

なぜ、かけるんですか?

絵をかくとわかりやすいので、かいてみましょう。
状況をシンプルにまとめるとこのような樹形図になります。


樹形図って、木みたいだからですか?

そうです。ではなぜ、かけ算になるかを見てみましょう。説明のために、鍵には【1】~【12】の番号をつけます。図と照らし合わせて、考えていきましょう。

まずは、1つ目の鍵穴にセットする鍵を選ぶんですね。

そうです。12通りありますね。ここでは、鍵【1】をセットしましょう。

残りの鍵は、【2】~【12】までの11個です。

では、2つ目の鍵穴に、鍵【2】をセットしましょう。

残った鍵は、【3】~【12】番の10個です。

ここからが重要です。鍵を【1】と【2】と選んでいるとき、3つ目の鍵穴にセットする鍵の選び方は、何通りありますか?

残った鍵の個数、10通りですね。

そうです。さらに、【1】‐【3】と選んだ場合は? 【1】‐【4】と選んだ場合は?

それぞれ、3つ目の鍵の選び方は10通りですね。そうか、10通りの選び方が、2つ目の鍵穴の11通り分だけあるから、2番目と3番目の鍵穴については、11×10通りですね!

その通りです! こうして、かけ算になります。そして、1つ目の鍵の選び方が12通りあるので…。

【1】‐【 】‐【 】、【2】‐【 】‐【 】...、【12】‐【 】‐【 】のそれぞれに、11×10通りの鍵の選び方が続くから12×11×10=1320になるんですね!

はい。このように「連続で起きていること」「順番があるもの」を「順列」といいます。

公式はありますか?

分子はnから大きい順に数字をr個かけ合わせます。公式では nPr と書きます。
異なるn個のものから異なるr個のものを順列で取り出すという意味です。(Pは、英語の “permutation” (パーミュテーション)から来ています)

むむっ。それ…PとかCとか、うっすら記憶はあるけど、めっちゃ苦手でした…

ここで、少し得意になりましょう。先輩の場合は、12個の鍵から番号の付いた鍵穴にそれぞれ正しい3つの鍵を選ぶので、12P3=12×11×10=1320になります。
そういえば、キャビネットに何が入っているのですか?

お菓子らしいです。お客様から珍しいお菓子をいただいて、
組み合わせCの考え方

順列の考え方がわかってきましたね。Cという言葉も出てきたところで、組み合わせについて学んでみましょうか。

Cですね。

では、簡単な問題を用意しました。A、B、C、D、Eさんの5人から2人を選びます。最初に選んだ人にガムを、次の人にチョコを渡します。何通りの選び方ができますか?

えーと、ガムがもらえる候補が5人で、チョコがもらえる候補は...ガムをもらった人を除くので4人。だから、選び方は5×4=20通り! これは、先ほどのPの考え方ですよね?

その通りです。では今度は、この5人から、アメを渡す2人を選んでください。

2人選んでどちらにもアメを渡すなら...順番は関係なくなりますよね?

すばらしい着眼点です。そうなんです。A-Bさんを選ぶのと、B-Aさんを選ぶのは同じ意味になります。このように、選ぶ順番を区別しない選び方の通りを「組み合わせ」といいます。

これがウルトラC。

そうです。Combination(コンビネーション)ですね。順列で求めた数から、A-B、B-Aのような同じ要素による並び順の違いを除外する必要があります。
考え方が難しいので、まずは組み合わせの考え方を樹形図で確認しましょう。
組み合わせは下のようになります。
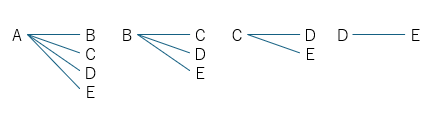

10通りが答えですね!これも計算できるんですか?

2人の並び順は 2! (=2×1=2)通りあるので、順列の総数を2!で割ることで組み合わせの数が得られます。

なんか難しいですね。2の「びっくり」はなんですか?

これは階乗(かいじょう)といって、その数から1までのすべての整数をかけていくんです。たとえば、2!=2×1ですね。これで割るので、組み合わせの計算式は次のようになります。
nPr/r!=5P2/2!

うーん、ややこしい。ところで、ウルトラCはどこに行っちゃったんですか?

組み合わせの公式には「C」を使いますnPr/r!=nCr という関係があって、n個の中からr個を選ぶときに使う公式です。

計算方法はどうなるんですか?

分子はnから大きい順に数字をr個かけ合わせ、分母はrから1までの数字をかけ合わせます。

言葉が脳に刺さりません!

では具体的に。5人から2人の組み合わせを選ぶ5C2は、5×4/2×1です。つまり分子はnから大きい順にr個のかけ算、分母はrから1までの数字のかけ算...

あ! 確かに、nPr/r! の形になっている! びっくりが出てきたときは、全然わからなかったのですが、Cの公式だと思うとちょっと気分が楽になります。

まあ、Cを公式として覚えてしまってもいいでしょう。ただ、公式を暗記する前に、理屈を理解しておくと、さらに覚えやすくなりますよ。
ITパスポートの問題に挑戦!

ITパスポート平成23年度 秋期 問37 に挑戦しましょう。
問37 インタフェースを一つだけもつモジュールが6個ある。これらのモジュールが相互に結合できるかを試験したい。1組のモジュールの結合テストに4時間を要するとき、すべての組合せのテストに合計何時間かかるか。
選択肢: ア 20 イ 24 ウ 60 エ 120

も、問題文の意味がわからないです…。

身近な例で考えてみましょう。6個の部品があって、これらの部品が正しく組み合わせできるかを確認したい場面です。レゴブロックのように、それぞれの部品が他の部品とちゃんとくっつくか、それを確認する作業と考えてみてください。

では、まずは、部品の組み合わせの数を出せばいいんですね。

その通りです。6個の部品から、相互に結合するので、2つ選ぶということになります。

さっき習った方法で計算すると...
6C2は、6×5/2×1= 15通りですね!

すばらしい! そして1組の組み合わせのテストに、4時間かかると書いてありますね。

となると、15×4=60時間です! 答えは「ウ」!

よくできましたー! 「順番が大切なのか」「順番は関係ないのか」を考えることで、PとCを使い分けることができます。順列(P)は「順番が大切」、組み合わせ(C)は「順番は関係ない」と覚えておくといいですよ。

よくわかりました。いずれにせよ、先輩の1320回の鍵合わせはやっぱり手伝わなくてよかったです。

それはそうですね。では、お疲れさまでした。
ポイント
順列(P)と組み合わせ(C)の違いは「順番」
- 順列:順番が大切!(ガムを先にあげる、チョコを先にあげるは別物)
- 組み合わせ:順番は関係なし(2人選ぶだけなら、誰が先でも同じ)
計算方法
- 順列(nPr):最初の数から順番にかけていく
例:12個から3個選ぶ → 12×11×10 - 組み合わせ(nCr):順列の数を並び替えの数で割る
例:5人から2人選ぶ → (5×4)÷(2×1)
今日の問題をおさらい
Q1. キャビネットの鍵問題(順列)
鍵穴が3つ、鍵が12個あります。3つの鍵穴に正しい鍵が同時にセットされないと扉はあきません。最大試行回数は?
12P3 = 12 × 11 × 10 = 1320
答え:1320回
Q2. ガム・チョコ配り問題(順列)
5人から2人選び、最初の人にガム、次の人にチョコを渡す場合の組み合わせは?
5P2 = 5 × 4 = 20
答え:20通り
Q3. アメ配り問題(組み合わせ)
5人から2人選んでアメを渡す場合の組み合わせは?
5C2 =5×4/2×1= 10
答え:10通り
Q4. ITパスポート試験問題(組み合わせ)
インタフェースを一つだけもつモジュールが6個ある。これらのモジュールが相互に結合できるかを試験したい。1組のモジュールの結合テストに4時間を要するとき、すべての組合せのテストに合計何時間かかるか。
選択肢: ア 20 イ 24 ウ 60 エ 120
6個から2個選ぶ組み合わせ:6C2 = 6×5/2×1 = 15通り
1組4時間かかるので:15 × 4 = 60時間
答え:60時間 (選択肢 ウ)