前回は、わかりやすい棒グラフ作成のポイントと棒グラフの限界について説明しました。今回は時系列データの表示でよく用いられる折れ線グラフを取り上げます。
折れ線グラフは「比較」よりも「変化」を見せるのに適している
今回は折れ線グラフを扱います。第2回でもお話ししたように、折れ線グラフは基本的に時系列データを表示する場合に最も優れていますが、項目間の比較をする場合に棒グラフの代わりとして利用することもあります。前回(第4回)の棒グラフのところでご紹介した図を、折れ線グラフと比較して見てみましょう(図1、図2)。どちらもそれほど違和感はありませんが、棒グラフはやはり隣接した棒同士の違いが強調されますし、折れ線グラフは項目間の変化・違いの方が前面に出てくるという違いはあります。
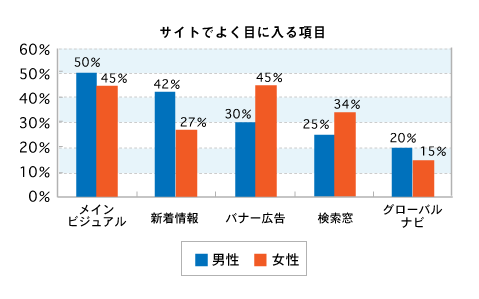
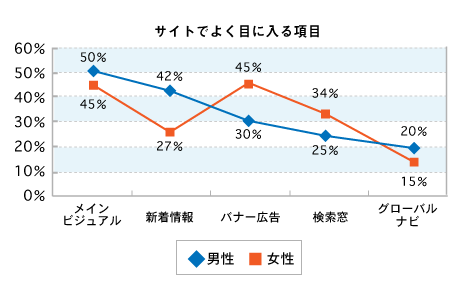
系列が3つ以上になると見やすくするために折れ線グラフを使うことも多いですが、各項目の系列間での比較をする場合は、多少見づらいですが集合棒グラフにした方が目的にかなっています(例えばアンケートのある質問項目を年代別に表示するような場合、10代から60代まで6本の棒が隣り合わせに立ちます)。どのグラフを選ぶか迷った時の判断については、次回詳しく触れたいと思います。
折れ線グラフは時系列データの分析に威力を発揮する
継続は力なりと言いますが、調査データは継続的に追ってこそ、意味深いものになります。アクセス解析などでも単月データだけでは、それがよい方向に向かっているのか、悪い方向に向かっているのか判断できません。もちろんある時点のアクセス解析のデータだけを見ても、たとえば直帰率が悪い部分などはすぐに発見できるので、局所的には改善施策を講じることもできるでしょう。しかしそれは一過性の対症療法で終わってしまいます。
1年間以上データが蓄えられていれば、季節変動や対前年同月比がわかりますし、折れ線グラフで見ることで、上昇下降という方向に加えて、その勢い、言い換えると加速度が見て取れるということが大きなメリットと言えるでしょう。データを蓄積するのには時間がかかる場合が多いですが、この継続性こそが大変重要なのです。
図3はYahoo! JAPANの過去3年分の1日当たりのページビュー数を、発表資料のデータをもとにグラフ化したものです。年別に系列を分けて作図した意図は季節変動の発見にあります。残念ながら、それほど特徴的な季節変動は見えてきませんでした。もう1つの見方は2006年から2007年と2007年から2008年の比較です。青線(2006年)と橙色線(2007年)の間隔に比べると、緑色線(2008年)と橙色線(2007年)の方が接近しているので、2006年から2007年の伸びの方が大きく、2007年から2008年は成長が鈍化しているという事実がわかります。
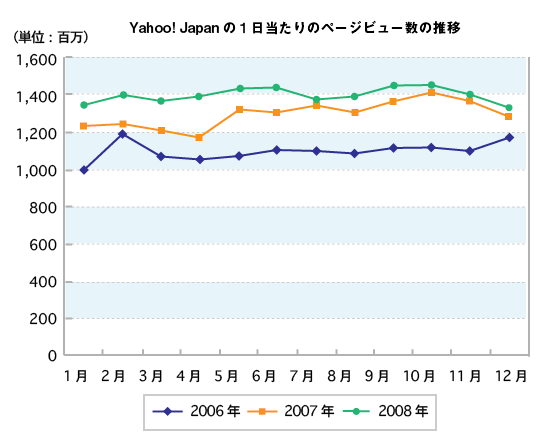
こういう見方をすることで、たとえばこれからはPV数の伸びはあまり期待できないので、滞在時間を伸ばすことに戦略をシフトするであるとか、次の方向性を考えるヒントになるはずです。過去と比較する以外にも、目標値をこの折れ線グラフに追加することで、異なるベンチマークとの比較も同時に行うといった方法が採れます。過去との比較も1つのベンチマークとの対比をしていることになるわけです。
縦軸の目盛を操作して変化を大きく見せるトリック
さて図4は第1回で、小さな変化を大げさに見せるトリックとして紹介したのと同じものです。縦軸の目盛をゼロ以外の数字から開始するこのトリックは棒グラフでも使える手法ですが、折れ線グラフで見ることが多いように思えます。折れ線グラフは時系列推移を示すことが多いためでしょうか。棒グラフではボリュームの違いを比べるのは2、3個あれば十分で、その部分を誇張するためにこのトリックを使ってもすぐにバレルという訳です。
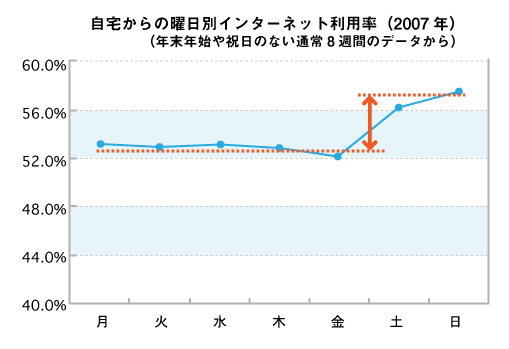
縦軸が0%からではなく40%から始まっていることに注意
最近読んだある洋書には、目盛をゼロから表示しないこの表示方法は、棒グラフでやってはダメだが、折れ線グラフでは問題ではないと書かれていました。確かに変化を詳しく見せるという趣旨を踏まえたうえで、その変化をズームしてみせるということであれば問題ないかもしれません。しかし、グラフを見る人が見誤る可能性を少なくするためにも、できるだけ同じ原則を適用するのがよいと私は考えます。そうでないと際限なくズームしてしまうことも認めてしまうことになるからです。
横軸の幅を操作して伸び率を大きく見せるトリック
図5をご覧ください。これは架空の数字から作成したグラフですが、あるトリックを使っています。2008年一年の伸びは目覚ましいものがありますが、さてここで利用したトリックとは何だかおわかりでしょうか。これも折れ線グラフの特性を生かした代表的なトリックです。
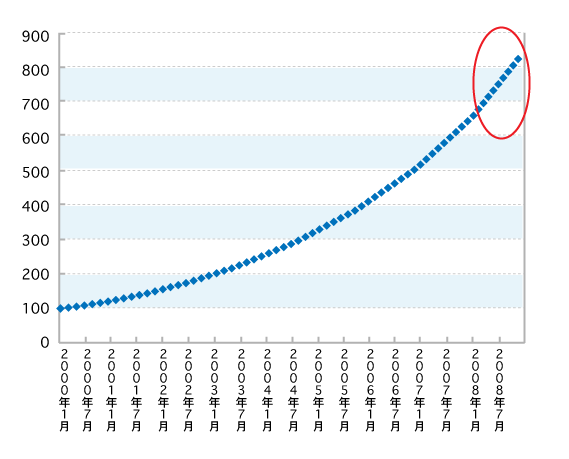
このグラフは、最初の2000年1月を100として毎月2%ずつ増加するような数字をもとに作図した折れ線グラフです。2000年から順調に成長していて、2007年ぐらいから伸びが大きくなり、さらに2008年の1年間はグラフの傾きが45度ぐらいの急勾配になっているため、一段と急激に成長しているように見えます。繰り返しになりますが、伸び率は毎月2%で完全に一定なのです(ただし、この例は複利で増えるので、正確に言うと指数関数的に増加してはいますが)。そこで2008年の1年間だけを別途抽出したグラフ(図6)を見てみてください。まったく別の印象を与えるグラフになります。
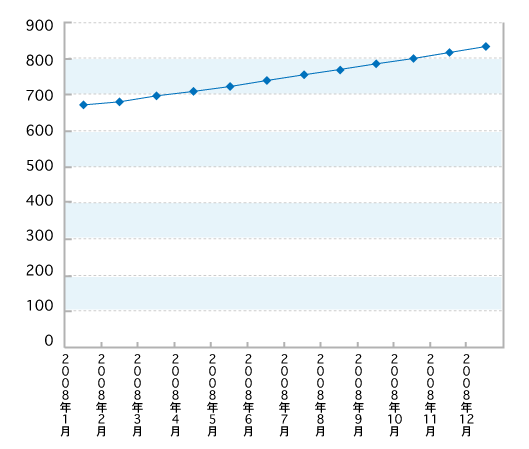
図6はグラフの傾きがなだらかで、急激に伸びているようには見えません。そうです、今回使ったトリックは、目的とする期間を短縮して見せる(横軸上での幅を相対的に短くする)ことで、変化率を大きく見せるというトリックです。図5では、横軸の2008年1月が少し右に寄っているため、2008年1月と2008年7月の距離がほかよりも短くなっているのです。
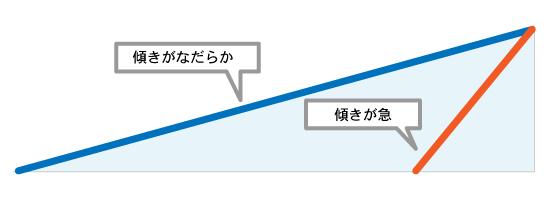
高さ(縦軸方向の変化)が同じでも、底辺(横軸の期間)の長さが短くなれば、斜辺の傾き(グラフの勾配)が大きくなるという図形の性質を利用したトリックというわけです。このように折れ線グラフでのトリックは変化を大きく見せるということに尽きます。
まとめ
時系列推移を表示した折れ線グラフは、1年間以上データが蓄えられていれば、季節変動や対前年同月比がわかりますし、上昇下降という方向と加速度が見て取れるということが大きなメリットです。多くの情報をコンパクトに表示し、しかも多くの示唆を与えられるのが、時系列折れ線グラフの特徴です。ぜひロングスパンのデータ分析に多用してください。
折れ線グラフでよく使われるトリックは、大きく2つあると覚えておきましょう。1つ目は縦軸をゼロから表示しないことによって、変化を過大に見せる手法。2つ目は横軸上の該当期間を意図的に短くすることで、変化を過大に見せる手法。いずれにしても、変化を過大に見せるというところで、折れ線グラフの特徴を最大限生かした方法と言えます。自分で意図的に使う際にはほどほどに、他の人が使っている場合はパッと見でだまされないようにしましょう。