【計算できる？】平均売上5000万円、佐藤さんの売上5000万円、彼の営業成績の偏差値は？｜意外と理解していない偏差値

アユムさん、何の記事を読んでるの？

英語の勉強を始めたんだね。ところで、その偏差値70の人は、どこで偏差値が70？

それはそうだよ。偏差値は、母集団の平均で変わるんだから。
では問題。第1営業部の平均売上が5000万円、佐藤さんの売上が5000万円のとき、佐藤さんの営業偏差値はいくら？

計算をしなくても、佐藤さんの営業偏差値は50だね。

偏差値は頑張りとか、目標達成とか関係ないので、山田さんの偏差値は50以下だね。

お、今日は少し、高度な内容ですね。偏差値は、その集団（＝母集団）の中である人（数値）がどの位置にいるかを、平均を使って相対的にあらわし、比較できるようにした指標です。

募っていない、とはいえませんが、違います。母集団とは、対象の人や物の集まりを指す言葉です。

そうですね。もし、みんなが素晴らしい売上を上げていて、その母集団の平均売上額が高ければ、ある人が営業成績を伸ばしても、相対的にその人の偏差値は低くなります。

はい、おっしゃる通り。母集団の平均によって偏差値が変わります。

まあ、そこはいわゆる鶏口牛後、悩みどころですね。母集団の中で平均点より低かったら、偏差値は50以下になります。偏差値だけで考えたら、平均点が自分の点より低い集団に行けば、偏差値は高くはなりますね。

あるいは、隣のクラスとの期末テストの結果など、ほぼ同じ条件で測る偏差値で考えたら、ここまで見てきたように、平均点が自分の点より下の集団にいたほうが、偏差値は高くはなります。

うーん、それはどうでしょう。繰り返しますが、それはあくまで同じ集団における評価です。A組が特進クラスで、B組が普通クラスだったとして、偏差値が上がったとしても、アユムさんの本来の実力は変わっていないですね。

その通り。もちろん、状況によってはB組で優秀な結果を残したほうが、のちのち伸びる可能性もあるので、この例でも何が正しいかは判断できません。
ちなみに、私の姉妹の平均身長は150cmで、私も身長が150cmなので姉妹内では平均的、偏差値も50です。しかーし、全国的にみると同じ年代での身長偏差値は32.5と言われてちょっと驚いています。

（そんなことを言ったのは誰だ…。）ここまでで、偏差値は母集団の中での相対的な位置を表すものだと理解していただけたかと。

計算式は次の通りです。
偏差値＝（個人の得点 - 平均点）/標準偏差×10＋50

テーマも難しいので、無理にギャグを挟まなくていいですよ。標準偏差とは、データのばらつきのことです。偏差値を求めるには、その母集団の中でデータがどれだけバラついているのかを知る必要があります。

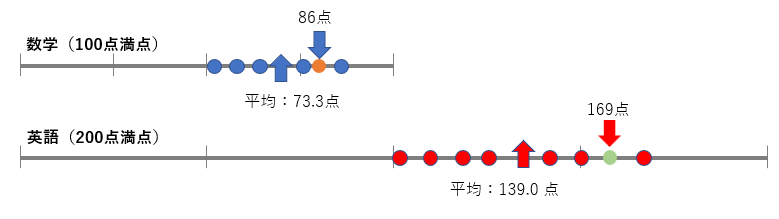
たとえば、数学と英語のテストの結果があるとします。数学は100点満点、英語は200点満点です。数学の点数の平均は73.3点、英語の平均点は139.0点です。Aさんは数学が86点、英語が169点でした。Ａさんは数学と英語、どちらのほうが偏差値が高いといえますか？

その通り。データのばらつき、つまり標準偏差がわからないと相対的な位置はわかりません。だから、この段階では、偏差値は求められません。

標準偏差を求めるには、分散という値を求めます。分散は、各データから平均を引いた結果を2乗し、それらをすべて足してデータ数で割った値です。

大丈夫です、一つずつ説明しますね。まずは、散らばりを求めます。散らばりは、それぞれのデータが平均からどれくらい離れているかで測ります。そこで、それぞれのデータから平均を引き、距離を求めます。

いい視点ですね。そのために2乗するのです。

この計算で得られた値をすべて足して、データの数で割ります。

これが分散です。ただし、これは2乗した値の平均です。

ひかえぃ～。ようやく標準偏差の登場です。標準偏差は、分散の正の平方根をとります。

Excelを使えば、STDEV.P関数で簡単に標準偏差を計算できますよ。

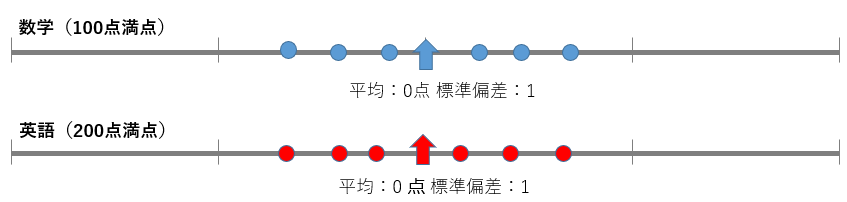
それでは、ようやく、偏差値を求めましょう。たとえば、数学と英語のテストで満点が異なる場合（100点と200点）、そのままでは比較できません。そこで、比較するために平均点を0点にし、標準偏差を1にします。

「1にする」「1とおく」という考え方は、この連載でも扱ってきましたね。

はい。ここでも標準偏差を1として、対象となる数値がどれだけ離れているかを出します。これを「標準化」と言います。そして、得点を標準化したものを「標準得点」と言います。

標準化された値は（データ － 平均値）/ 標準偏差 で求められます。

はい、標準偏差のいくつ分離れているかを計算するので距離の「もとになる量」は標準偏差ですね。平均から標準偏差がいくつ分離れているかということです。

その変さ値が「標準得点」です。そして、これから、変さ値を偏差値に変えましょう。なんか私、今、うまく拾いましたね（自画自賛）。

標準得点は値が小さいので10をかけ、大きくして、どれだけ離れているかの差をわかりやすくします。また、アユムさんの言うように、マイナスになってしまうこともあるので、真ん中（平均値：もともと0点）が50になるように+50をします。

母集団のデータ分布を「正規分布」といって、平均値を頂点とした山型となり、あとはなだらかに左右対称であるとき、偏差値60は、上位約16％です。
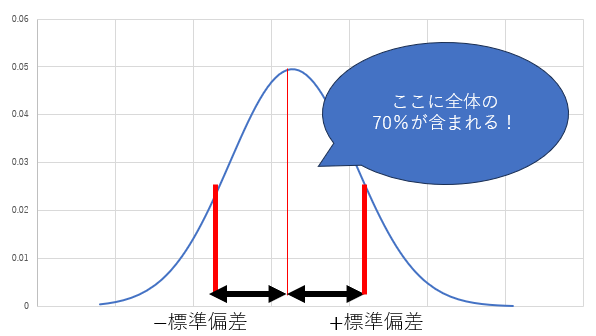
また、偏差値40～60の間に、全体の約70％が含まれます。

正解です！ そして、平均から標準偏差2つ分離れた範囲（上図の太い赤線とグラフの部分）は、全体の約95.4%であることが分かっています。つまり、95%あまりの人が、平均点から標準偏差2個分の範囲に収まっています。

え、ちょっとだけ？

なんでもかんでも偏差値という言葉を使うのって、ナンセンスですよね。

まず、適当に言っている偏差値は気にしない。数字がないものは論外です。

そして、母集団にある程度の人数がいないと、相対的な位置に意味がありません。だから、母集団の性質や人数をきちんと確認する。

全国偏差値のようにデータが多い場合、正規分布に近くなり、偏差値はより正確になります。学内偏差値は、状況次第ですね。データが十分な人数だけあるのか、きちんと正規分布をとるデータなのか、そもそも試験の内容が適切なのかも関係してきますね。

左右対称の分布でない場合は、偏差値を感覚的に使えないのでお薦めしないですね。

たとえば、15人のクラスで、1人だけ100点で、残り14人が0点のテスト結果があったとしましょう。偏差値を求めると100点の人が偏差値87.4で、残りの人は47.3です。この偏差値に何か意味がありますか？