回答「数」が多い調査と、回収「率」が高い調査、どちらが信頼できるか?
前回、調査対象者を選ぶときにはランダム性が重要であるという話をしました。そうしないとサンプルが偏るためです。しかしサンプル自体が偏っていなくても、実際の回答者が偏っているとやはり使えない調査となってしまいます。
数字を絡めた具体例でお話します。次の2つの調査を比較してみましょう。
- サンプル数10万人(無作為抽出)、回答数1万人の調査(回収率10%)
- サンプル数1000人(無作為抽出)、回答数900人の調査(回収率90%)
(1)「回答数は多いが回収率が低い調査」と、(2)「回答数は少ないが回収率が高い調査」のどちらがより信頼できる調査結果を得られると考えますか?
どちらもランダム性においては同条件で問題ありません。サンプル数、回答者数を比較すると、どちらの数字も(1)>(2)ですから、(1)の調査の方が良さそうに見えますが、実はこの場合は回収率が高い(2)の調査の方が、全体の誤差が少ない良い調査だと言えます。その理由を説明していきましょう。
回収率が低い場合に起こりうる調査結果の偏り
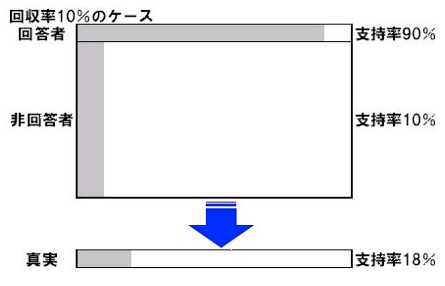
(1)の調査で回答した10%(1万人)の人たちのうち90%(9000人)が、ある問いに対して「はい」と答えたとします。つまり、この調査結果では、この問いの支持率は90%ということになります。
ここで、回答しなかった人90%(9万人)の答えを知る術はありませんが、仮に「はい」と答えた人が10%(9000人)しかいなかったと仮定します。そうすると、合計した全体の「はい」と答えた人の実態(図では真実と書きましたが)は、10万人中1万8000人(9000人+9000人)なので、支持率18%となります。これは調査結果の支持率90%と大きな差があります。
このように回収率が低い調査の場合、もし非回答者の答えが回答者と大幅に違っていた場合には、調査結果に大きな誤差が出る可能性があるのです。
一方、回収率が90%と高かった(2)の調査はどうでしょうか。(1)のときと同じく、ある問いに対して回答者(900人)の90%(810人)が「はい」と答え、非回答者(100人)では10%(10人)しか「はい」がいなかったと仮定します。この場合、目に見える調査結果としては支持率90%となりますが、1000人中「はい」の割合は820人(810人+10人)なので、合計した全体の実態は、支持率82%となります。
(1)と(2)では、回収率以外は回答者の支持率、非回答者の支持率が同じだったにもかかわらず、結果は正反対になりました。
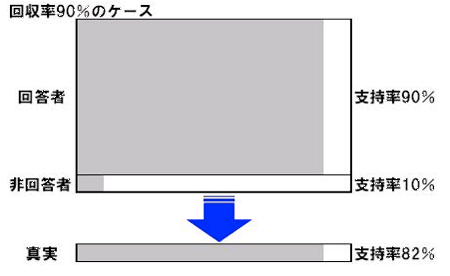
(1)の回収率10%の調査では、調査回答による集計結果である90%と真実の18%に大きな隔たりがあります。一方、(2)の回収率90%の調査では、調査回答による集計結果である90%と真実の82%に大きな隔たりはありません。つまり回収率(協力率)が低いと、調査結果に偏りが出て、真実と乖離してしまう可能性が高くなるということです。
回収「数」よりも回収「率」の高さが重要
ここからわかるのは、回収数の多寡より回収率の方が重要だということです。上の例でご紹介したとおり、真実と近かった調査結果は、回収率の高い(2)の調査でした。信じたくないでしょうが、サンプル数も回収数も圧倒的に多かった(1)の調査が、大金を掛けてゴミを作った調査となってしまったのです。
偏りを避け、無駄な調査をしないためには、調査の回収率(協力率)が高いことが重要です。私が20年前に教わった頃は、偏りのない調査のためには「回収率6割を目指せ」などとも言われましたが、現在一般の調査でこれ程の高回収率を望むのは難しいと思います。
しかし、調査実施主体側からすると、なるべく高い回収率を目指すことが求められますし、調査を依頼するクライアント側の立場では、この回収率が調査結果の品質をチェックする上での重要な指標の1つになると覚えておきましょう。ただし、これはあくまで、政党支持率のような絶対値の精度が求められる調査の話です。
協力率が低いことに伴う「偏り」を避けるには?
今回の例は非回答者の支持率が回答者の支持率と大きな違いがあったので、極端だと思われるかもしれませんので、もう1つ例を挙げてみます。たとえばインターネットの動画サービスに関する調査をするとします。いきなり動画の質問をすれば、そもそも「私は関係ない」と思った人は調査に協力するとは思えません。
それではどうするかというと、まず調査依頼のタイトルに「インターネット動画に関する調査」と書かないことです。タイトルは「映像に関する調査」とでもします。そしてあたりさわりのない質問の後に、いよいよ「あなたはブラウザで動画を見たことがありますか」といった質問をするわけです。
そうすれば、インターネットで動画を見ていない人も回答するので、全体の動画閲覧率も実態に近いものになるでしょう。動画に関心のない人がそもそも協力しないことで、実態より動画閲覧率を高くしてしまうリスクを軽減できます。
誤差を半分にするにはサンプル数が4倍必要
普通は誰でも、サンプルあるいは回収数が多ければ多いほど、直感的に調査の精度は高くなると感じますが、実は回収率という要素の方が大事だということは、おわかりいただけたと思います。これは以下でお話しする標本誤差以上に、回収率が低いことによる偏り(これは非標本誤差の1つです)が、圧倒的に全体の誤差に影響を与えるからです。
回収率を上げる方法のほか、サンプル数を増やすことでも誤差を少なくすることはできます。ここで誤差を縮めるためにどれぐらいサンプル数を増やせば良いのかをはじき出す計算式を紹介しましょう。本連載で唯一の計算式です。
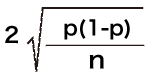
n=サンプル数、p=ある質問に対する回答比率
「2」は信頼度95%の係数1.96の近似値
これはサンプル調査の誤差を表す式です(厳密にはもう少し複雑ですが、母集団が大きい場合はこれで近似します)。正式には「標本誤差」と言います。たとえば、ある調査のサンプル数が1000だったとします(この式ではnが1000になります)。そしてある質問に「はい」と答えた人の割合が30%だったとします(pの値が0.3となります)。
つまり調査結果は「はい」が「30%」だったのですが、真実は「30%± ![]() 、すなわち30%±2.9%」ですよ、ということです。ただしこの誤差の範囲は95パーセントの確率でこの幅の中にある(95%の信頼度)という係数の場合です。100回のうち99回同じ調査をやってもその幅に入るようにする(99%の信頼度)場合は、2でなくこの係数が大きくなりますし、逆に90%の信頼度でいい場合はこの係数が低くなります。
、すなわち30%±2.9%」ですよ、ということです。ただしこの誤差の範囲は95パーセントの確率でこの幅の中にある(95%の信頼度)という係数の場合です。100回のうち99回同じ調査をやってもその幅に入るようにする(99%の信頼度)場合は、2でなくこの係数が大きくなりますし、逆に90%の信頼度でいい場合はこの係数が低くなります。
統計学の連載ではないので難しい話はこのくらいにしておきます。よく使われるのは信頼度95%のケースのこの計算式だということを知っておけば十分です。
回収率が低いといった理由で生じる「偏り」とは違って、こちらは確率論で計算できる世界の話になります。この計算式の構造を見てもわかるとおり、確かにサンプル数が大きいことが「誤差」を少なくしているということがわかります。
しかしルートが掛かっているので、誤差を半分にするにはサンプル数を倍にするのではなく、その二乗の4倍にしなければなりません。逆の言い方をすれば、サンプル数を倍にしても、誤差は3割程度しか減りません。この原則だけは覚えておいてください。
視聴率20%のテレビ番組の本当の視聴率の値は?
計算式を覚えるのも手間なので、下の早見表があれば十分です。調査データをよく見る人は手帳にでも下表を貼っておくとよいでしょう。
| サンプル数 | 回答比率 | ||||
|---|---|---|---|---|---|
| 10%または90% | 20%または80% | 30%または70% | 40%または60% | 50% | |
| 10,000 | ± 0.6% | ± 0.8% | ± 0.9% | ± 1.0% | ± 1.0% |
| 5,000 | ± 0.9% | ± 1.1% | ± 1.3% | ± 1.4% | ± 1.4% |
| 1,000 | ± 1.9% | ± 2.5% | ± 2.9% | ± 3.1% | ± 3.2% |
| 500 | ± 2.7% | ± 3.6% | ± 4.1% | ± 4.4% | ± 4.5% |
| 100 | ± 6.0% | ± 8.0% | ± 9.2% | ± 9.8% | ± 10.0% |
実際この早見表を使って、誰でも知っているテレビ視聴率を素材にして計算してみます。関東エリアで、ある番組の世帯視聴率が20%だったとします。テレビ視聴率も実は世帯、個人での区別や、番組平均や瞬間視聴率などさまざまなものがあります。そのままこの表を適用してよいかなどの細かい議論は今回は飛ばします。
関東エリアの調査世帯数は600ですから、表で「サンプル数」が500の行で、「回答比率」が20%か80%の列が交差する部分を見ます。±3.6%とあります。実際のサンプルは600なので、3.6%より少し少ないはずですが、20%±3.6%とすると、16.4%から23.6%となり、意外と幅が広いことに驚いたと思います。
調査費用と調査サンプル数
さて最後に調査費用について考えたいと思います。調査には費用が掛かります。テレビ視聴率の例で意外と誤差が大きいと思われたかもしれませんが、誤差を半分にしたければ、サンプルは4倍にしなければなりません。全体の費用が単純に4倍になることはありませんが、調査協力世帯の抽出や謝礼、維持コストは、ほぼ4倍掛かるでしょう。集計費用も、日記式であれば集計作業は手作業となり、量に比例すると思われます。
各種効率化の工夫はあるにせよ、誤差を半分にするためには費用は倍増以上となります。最終的にはクライアントがどの程度の精度の調査に対してどれだけの費用を払えるのかというところに落ち着きます。
「そんなに誤差があるなら使えないじゃないか」と周りが言うのは勝手ですが、クライアントはこの貴重な情報をもとに、よりよい番組作りや、効果的な広告作りのためにがんばっているはずです。
調査費用を払っていない我々は、出てきたデータを楽しめば、それで良いのではないでしょうか。
調査概要が書かれていない調査は信用できない
ここまでで読者の方にできる簡単なチェック方法をお教えします。今までお話したいくつかのポイントをみるだけのことです。
何かの調査データがあったら、必ず原典にあたってください。まず公開されたリリースがなければ話になりません。そしてそのリリースの中に調査概要が記載されているかどうかを確かめましょう。これらが無ければ、どういう品質の調査かすらわかりません。
例:
- 調査対象者は誰か(日本全国の18歳以上の男女)
- 対象となったサンプル数は何人か(2000人)
- 回答者の数は何人で、回収率は何%か(1200人で回収率60%)
- 代表的な回答者属性は(男女比が54:46)
次回は「データの収集方法とチェック」について説明します。
- より回収率が高い調査の方が信頼できる
- 回収率が低い場合には調査結果の偏りが起こりうる
- 回収「数」よりも回収「率」の高さが重要
- 協力率が低いことに伴う「偏り」を避けるには、調査のタイトルの付け方が重要
- 誤差を半分にするにはサンプル数が4倍必要
- 視聴率20%のテレビ番組の本当の視聴率の値は16.4%から23.6%
- 調査サンプル数に比例して、調査費用は増える
- 調査概要が書かれていない調査は信用できない