【計算できる?】付箋40円、メモ帳60円。予算は47000円、合計1000個の場合、それぞれいくつ買える?
算数が苦手な新米マーケターのアユム。今回は、予算と合計個数がわかっている状況で、付箋とメモ帳の購入数を「鶴亀算」で求めていきます。
2024年5月27日 7:00
40円の付箋と60円のメモ帳。予算に応じて、それぞれの購入数を求めよう!

今度の新商品の発売開始に合わせてクライアントに配布する記念品を作る予定なんだけど、何がいいかな?

ダンゼン、実用的なものがいいですね。今までいただいたものとしては、付箋とメモ帳がうれしかったです! ノベルティショップのサイトを見たところ、付箋が40円、メモ帳が60円ですね。

なるほど。全部で1000個になるようにして、予算は47000円。そうすると、付箋とメモ帳、それぞれいくつずつにすればいいかな。

それぞれいくつになるんですか?

付箋が650個、メモ帳が350個だ。

!? どうやって求めたんですか?

じゃ、デザインの部門に相談してくるね! 求め方を考えておいてね~

え~
昔から、算数も数学も苦手なアユムは、希望が叶ってマーケティング部門に異動してきました。Web担で見るような「すごいマーケターになりたい!」と胸を躍らせていたが、配属後、理想と現実のギャップに苛まれることに。データ、数字、%、小数。うわぁーん、どうしたら、数字に強くなれるのでしょうか……。
そこに現れたのが、大人向け数学教室「大人塾」を運営し、数学苦手な社会人に対して指導をしているアジアゾウをこよなく愛するモリさん。

この記事を読むべき人: 数字の問いに答えるのが苦手な方
この記事を読む必要がない人:鶴亀算ができる方
この記事でわかること:ビジネスの世界で利用される鶴亀算
ビジネスで使える「鶴亀算」

記念品で、40円の付箋と60円のメモ帳、あわせて1000個、予算は47000円。いくつずつ発注すればいいですか?

付箋はいただくと重宝しますね。この問題は、いわゆる鶴亀算です。

これも鶴亀算なんですか? 税抜き価格を求めるところでやりましたよね。鶴と亀がどちらが先に山頂に行けるか競う問題。

まったく違いますね。それはウサギと亀です。

亀は競うのが好きなんですね。ところで、鶴亀算をすっかり忘れてしまったので、もう一度教えてください。

鶴亀算では、亀は競いません。今日は鶴亀算の解説です。まず、40円の付箋の数を𝒳とおきましょう。𝒳枚の付箋の金額はいくらになりますか?

40×𝒳=40𝒳円ですね。

では、全部でいくつで、このときのメモ帳の数はいくつですか?

全部で1000個なので、メモ帳は1000-𝒳(個)です。

さて、このときのメモ帳の金額は?

60×(1000-𝒳)=60000-60𝒳

付箋とメモ帳を足すと~

47000円! つまり、こういう式ですね
40𝒳+60000-60𝒳=47000

これを解いて~

13000=20𝒳 だから、𝒳=650! 付箋は650個ですね。

正解~! メモ帳は1000-650=350個です。
連立方程式を使って求めてみよう!

()を使った式って、かけ忘れたりして、間違えてしまうんですよね。

それでは、連立方程式で解きましょうか。

中学校で習いましたね。𝒳と𝒴が出てきた瞬間、敵が2倍になったように見えました。

𝒳、𝒴は敵ではなく味方ですよ。わからない数字をおきかえてしまえばいいのです。

だまされたと思ってやってみます。何と何を𝒳と𝒴にすればいいでしょう。

わからない数字はなんですか?

付箋とメモ帳の個数です。

では付箋の個数を𝒳、メモ帳の個数を𝒴とおきましょう。このときに、絶対に「何を𝒳、𝒴とおいたかは、忘れないようにメモ」しておいてください。

はい。

それでは、𝒳と𝒴を足すといくつですか?

𝒳、𝒴はそれぞれの個数なので、𝒳+𝒴=1000

次は金額です。それぞれいくらで、足すといくらですか?

付箋は40𝒳円、メモ帳は60𝒴円なので、40𝒳+60𝒴=47000です。

2つのわからない数字の式が2つできましたね。これで解けます。解いていきましょう。
40x+60𝒴=47000 は、全部の数字0をひとつ減らしましょうか。式がシンプルになり、間違いが減ります。
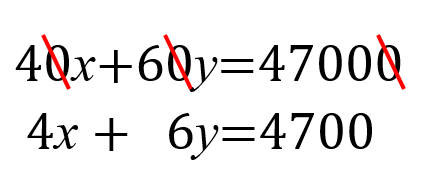

確かにシンプルですね。

次に𝒳+𝒴=1000 を確認します。この式を4倍するとどうなりますか?

4𝒳+4𝒴=4000 ですね。

はい、それでは上下に並べてかきましょう。「=」の位置をそろえましょう。

こんな感じですか? 4𝒳の文字がそろいましたね。
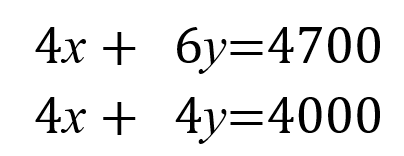

いいですね。それでは、上の式から下の式を引きましょう。

マイナス、プラスとか混乱しちゃうんですよね。
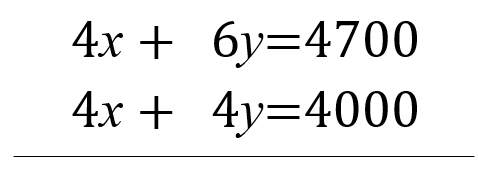

4𝒳-4𝒳=0、6𝒴-4𝒴=2𝒴 4700-4000=700 と個別に計算すると間違いが減りますね。

なるほど。となると、そろえることが大切なんですね。では、上から引きます。

これで𝒴=350 と解けました!

ですね。𝒳についても、𝒳+𝒴=1000から、𝒴に350を代入すると、x+350=1000、𝒳=1000-350=650と解けますね。連立方程式では、𝒳か𝒴についている数字(係数)のどちらかを2つの式で同じ値にして、それを引き算して消してしまえばいいのです。これを「加減法」といいます。

いい加減じゃなくて、加減法ですね! 連立方程式を解くときは、値をそろえて引けばいいんですね。なんか、ゲームみたい。
1個につき50円利益、不良品は110円損失。不良品の数はいくつ?

それでは今日の2問目です。下の問題に答えてください。
工場である製品を作ると1個につき50円の利益があります。不良品が出ると利益はなく、1個につき110円の損失になります。この製品を100個作ったところ、4200円の利益がありました。不良品は何個ありますか。

良品の個数を𝒳、不良品の個数を𝒴とおけばいいんでしょうか。

すばらしいですね。それでは、式を作ってください。

100個作ったので、良品+不良品=100、つまり、𝒳+𝒴=100…①
そして、あれ、不良品は1個につき110円の損失! これはどうすればいいんでしょう?

損失はマイナスであらわしましょう。

となると、良品の利益は50𝒳、不良品の損失は-110𝒴 となりますね。これを足して出るのが全体の利益なので 50𝒳-110𝒴=4200…②

利益が出てよかったですね。

②の式は、1の位のゼロをすべて消して5𝒳-11𝒴=420…②' とできますね。

では、上下にそろえてかきましょうか。

どちらを上にすればいいですか?

①の式を5倍すると、右辺(「=」の右側)は500になりますね。②’の式の右辺より大きくなるので、①の式を上にしましょうか。本当はどちらでもいいんですけどね。

こうですね。5𝒳-5𝒳=0はわかるんですが、𝒴はどうすればいいですか?
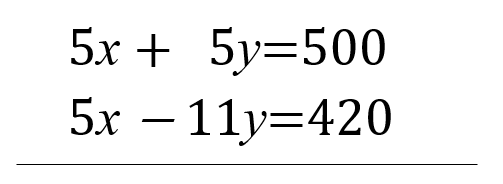

5𝒴-(-11𝒴) を解きます。マイナスにマイナスをかけるとプラスになるので、この式は、5𝒴+11𝒴になります。

そうだった! マイナスにマイナスをかけるとプラスになるんですよね。プラス思考の原点ですね!

思考は関係ないですね…。ではこれを解きましょう。

これでいいですか?
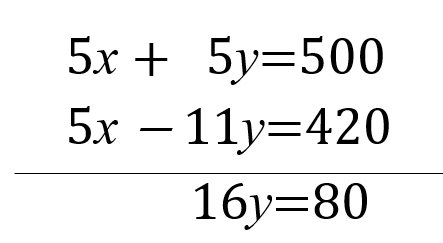
𝒴=5で、不良品は5個ですね! 𝒳、良品は100-5⁼95個ですね。よかった、そんなに不良品が出なくて…。

連立方程式を使って、鶴亀算をすっきり解けるようになりましたね。鶴亀算は鶴と亀の足の数だけじゃなくて、ビジネスにもいろいろ応用できます。身の回りの鶴亀算を見つけてみてください。

はーい。
ポイント
- 鶴亀算は、連立方程式でも解ける
- 何を𝒳、𝒴とおいたか必ずメモをする
- 連立方程式は、2式の𝒳か𝒴の数字(係数といいます)をそろえ、式から式を引いて解く
今日の問題をおさらい
Q1. 記念品で、40円の付箋と60円のメモ帳、あわせて1000個、予算は47000円。いくつずつ発注すればいいですか?
付箋の個数を𝒳、メモ帳の個数を𝒴とおく
𝒳+𝒴=1000
40𝒳+60𝒴=47000
𝒳=650、𝒴=350
答え:付箋は650個、メモ帳は350個
Q2. 工場である製品を作ると1個につき50円の利益があります。不良品が出ると利益はなく、1個につき110円の損失になります。この製品を100個作ったところ、4200円の利益がありました。不良品は何個ありますか?
良品の個数を𝒳、不良品の個数を𝒴とおく
𝒳+𝒴=100
50𝒳-110𝒴=4200
𝒳=95、𝒴=5
答え:不良品は5個