[特集]アクセス解析 “超” 基礎講座

報告の際に役立つ統計の基礎知識
「平均のひとつ覚え」から卒業
社会人なら知らなきゃ恥ずかしい統計の基礎知識
Web担当者が上司に自社サイトの状況を報告するときに必要になるのが、アクセス状況の概要だ。
経営陣が知りたいのはウェブサイトの細かいアクセス状況ではなく「全体像」。これを説明するときに使われるのが「データの特徴を表す代表的な数値」である。
報告会で突っ込まれたときに困らないように、社会人として最低限の統計の用語とその意味を正しく理解しておこう。こういった統計の基礎知識を知っていれば、アクセス解析のデータを正しく解釈するのに必ず役立つはずだ。
平均
代表的な数値としてわかりやすいのが「平均」だが、場合によっては平均では適切な解釈ができない場合がある。例を見てみよう。
図1は、横軸に日を、縦軸にその日の訪問者数を示した2週間分のグラフだ。
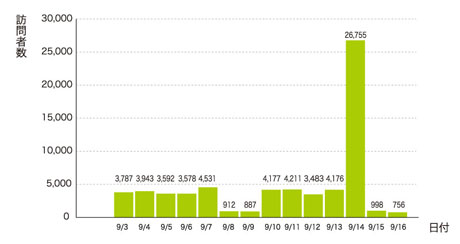
1日あたりの訪問者数を単純に平均すると次のようになる。
単純な平均訪問者数:4699人
しかし、このサイトは週末のアクセス数は平日の数分の1しかないため、平日と週末を分けて考えてみるのもいいだろう。そこで、平日と週末でそれぞれ平均を出すと、次のようになる。
平日の平均訪問者数:6223人
週末の平均訪問者数:888人
これで、平日は6223人より少なければ「アクセスが少なかった」、週末は888人より多ければ「アクセスが多かった」と判断していいのだろうか。
週末の平均はたしかに代表的な数値となっているが、どうも平日の平均がおかしい。グラフを見ても、ほとんどの平日は5000人以下と、平均よりも1000人以上少ないアクセス数になっている。
よく見ると9月14日のアクセス数が非常に多い。この日は、あるページがヤフーニュースで紹介されたために、非常に多くの人がサイトを訪れていたのだ。ヤフー以外にも人気のニュースまとめサイトなどで取りあげられると同じような現象になるし、だれかが作ったクロールプログラムが一気にサイト内のページにアクセスした大量アクセスが記録されたときも、このような「外れ値」が現れる。
平均を出すときには、こういった「外れ値」を除外して計算するべき場合もある。9月14日を除いた平均は次のとおりとなる。
外れ値を除いた平日の平均訪問者数:3942人
週末の平均訪問者数:888人
これで、適切な代表値を得られた。毎日のアクセス数を見て、3942人より多ければ平均以上だと考えて問題はなさそうだ。
平均の長所は、意味が明確で、対象となるすべてのデータを扱って算出される点。短所は、外れ値の影響を受けやすく、適切な代表値ではない場合がある点だ。
今回は特定の外れ値を人力で除外したが、上位数%と下位数%を除いた平均を出すといった「トリム平均」という方法もあり、競技で審判が出す得点の集計などで使われている。
中央値
代表的な数値をみる場合に、平均ではなく「中央値」を用いる方法もある。中央値は「メジアン」とも呼ばれ、データを小さいものから大きいものへと並べたときに、真ん中に位置する数値を指す(データが偶数個の場合は、真ん中の2つの値を足して2で割る)。
図1のデータから中央値を計算すると、次のようになる。
1日の訪問者数の中央値:3690人
中央値の長所は、長所として外れ値の影響を受けにくく、算出に複雑な計算を必要としない点。短所は、対象となるすべてのデータを扱って算出されるわけではない点だ。
大量のデータを順番に並べて真ん中の値を探すのは面倒だが、Excelにデータを全部入れて「=MEDIAN( )」のようにして関数を使うと瞬時に表示される。
最頻値
データを整理してよく見てみると、平均値や中央値が必ずしもデータ全体を代表しないことがある。たとえばサイトの滞在時間だ。1ページだけ見てさっさと帰って行ってしまう訪問者が多いので、平均では実態がわからないケースだ。度数分布表を作ってヒストグラムにすると、30秒以下と151秒~180秒の2か所に大きなピークがあることがわかる(図2)。
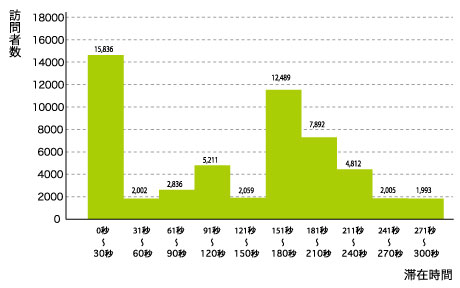
このようなピークを「最頻値」という。最頻値は「モード(流行値)」とも呼ばれる。
最頻値の長所は、外れ値の影響を受けにくい点。短所は、複数のピークがある場合に最大ピークだけを最頻値として扱うとデータの特徴を見逃してしまう点だ。
標準偏差
| 筆者Aの コラム | 筆者Bの コラム | |
|---|---|---|
| 955 | 2516 | |
| 1304 | 2751 | |
| 1493 | 2474 | |
| 7166 | 3110 | |
| 3047 | 2779 | |
| 1260 | 2665 | |
| 2141 | 2655 | |
| 3688 | 3251 | |
| 5866 | 3194 | |
| 1052 | 2697 | |
| 平均 | 2797.2 | 2809.2 |
| 最小値 | 955 | 2474 |
| 最大値 | 7166 | 3251 |
| 標準偏差 | 2173.7 | 277.6 |
代表的な数値がわかったとしても、それだけではデータの特徴を見逃してしまう場合がある。そこで、「データのばらつき具合(分散)」を判断する統計手法を1つ覚えておこう。
図3は、筆者Aと筆者Bが書いたコラムそれぞれ10本のPV数だ。それぞれのコラムの平均PVは次のとおりで、さほど大きな違いはない。
筆者Aのコラム:平均2797PV
筆者Bのコラム:平均2809PV
ところが、ばらつきを示す「標準偏差」を各筆者で求めると、次のようになる。標準偏差は、大きければ大きいほどばらつきが多いことを示すものだ。
筆者Aのコラムの標準偏差:2173.7
筆者Bのコラムの標準偏差:277.6
つまり、筆者Aは人気の出る記事を出すこともあるが当たらない記事もあり、筆者Bは大きなぶれがなくコンスタントにビューを集めていることがわかる。筆者Aにはよりヒットする記事を書いてもらうようにし、筆者Bには常連客以外も集める手段を考えるといいだろう。
標準偏差(Standard Deviation)を計算するには、Excelで「=STDEV( )」関数を使うのが簡単だ(図4)。ちなみに、標準偏差を手で計算する場合は、それぞれのデータで平均値との差を2乗した値を出し、それを合計したうえでそれを「データの個数-1」で割った値の平方根をとるという作業になる。
この記事は、あくまでもアクセス解析データでむやみに「平均」ばかりに頼ってしまうことに関して注意をうながし、難しいと思われがちな統計に興味をもってもらうための記事です。そのため、それぞれの指標や実際のアクセス解析で適した利用シーンなどまではつっこんで解説していません。
アクセス解析と統計に関して、ウェブアナリストの衣袋氏が記事を書かれているので、ぜひ参考にしてください。
また、統計に関する記事を衣袋氏に執筆してほしいというラブコールも歓迎です。多く集まれば(集まらなくても?)編集部から衣袋氏にオファーしたいと思います。




















