アポロニウスの問題の一つ「 1つの円に接し、2つの点を通る円(CPP)」の解までの作図手順
1つの円に接し、2つの点を通る円は、一般には下図のように二つの解がある。
1つの円に接し、2つの点を通る円は、一般には下図のように二つの解がある。
1つの点を通り、2つの直線に接する円は、一般には下図のように二つの解(青い円)がある。
2つの点を通り、1つの直線に接する円は、一般には下図のように二つの解がある。
3つの直線に接する円は一般には下図の通り、その3つの線の内接円が一つと傍接円が3つの合計4つの解が存在する。基本的な考え方は同じだが、念のため内接円と傍接円の場合とに分けて説明していこう。
よく使う作図パターンも用意できたので、いよいよアポロニウスの問題に一つずつ取り組んでいこう。基本原則としては、最初に与えられる 3種類のオブジェクトである点 , 線 , 円の 3つに関して、①線同士以外はお互いに交わっていないこと。つまり与点が別の与点 , 線 , 円線の上にあってはならないし、線が円と接しても交わっていてもいけないし、円同士が接しても交わっていないこと。そして②与円の中に他のオブジェクトが含まれないこと。つまり与円の内側に別の与円や与点があってはならないものとする。
それ以外の条件で、解の数が変化するような特殊解や解なしのケースがあれば、各問題毎に最後に触れることにする。また作図手順数は増えていくので、何段階かに図解を分けていくことになる(このページだけは非常に簡単なので例外だが)。問題別に、作図手順の他に考え方や解説を適宜交えてある。
本ページは、コンパスと定規で作図できる、頻出する基本作図パターンの手順を列挙したものである。10種類の問題別作図ページの解説内で、これらの基本作図パターンをよく利用するので、同じ作図手順を全部繰り返し書かずに冗長性を省きたいのだ。例えば「ある直線に対して、ある点から垂線を下ろす」という作図は 4手順必要だが、作図手順解説では「直線 l に対して、点Aから垂線を下ろす」の 1行で済ますということだ(もちろん作図手順を省略した旨は、必ず書き添えておくので、このページを見直して貰えばいい)。
なお、作図が細かくて見づらいものは、画像のリンクを新しい画面で表示すれば原寸大で見ることができるので、二つのページを交互に見るなどして確認して頂きたい。
・12の基本作図パターン
下記12個の作図課題の作図手順を一つずつ示していく。少なくとも前半の6つだけは、10種の問題別作図ページを見始める前に確認しておいて欲しい。なおページ内リンクは張ってないので見たいものがあれば、スクロールして見つけて欲しい。
このページでは、「アポロニウスの問題」10種の問題について全体像を概観するのと、コンパスと定規だけで作図するのにあたり、前提として利用している定理について触れることにする。
・「アポロニウスの問題」10種の問題を概観する
「アポロニウスの問題」のホームページでも触れたとおり、3種類のオブジェクト(点と線と円のこと)の組合せで作られる問題の種類は全部で10種類になる。
各列について簡単に説明していこう。まず「略称」だが、点、線、円の組合せの種類をいちいち「一つの直線と二つの点」のように表現するのは冗長なので、簡単に表す。それぞれ英語の頭文字をとって表現するだけのことで、円はCircleなのでC、直線はLineなのでL、点はPointなのでPだ。P , L , Cの表記のどれを優先するかは、人それぞれのようなので、LLPはPLLと表記することもあるようだ。
「解の数」は、各問題に対して答えとなる円の数の最大数のこと。例えば「解の数」が 4 と書いてある問題でも、オブジェクトの配置によっては解の円が二つしか存在しないといったことがある。
「作図手順数」は、定規とコンパスによる操作を何度行えば解に辿り着くのかの回数のこと。作図法は一つとは限らないので、それぞれの問題で提示した手順で作図した場合の凡その手順数である。どの程度作図が面倒なのかの一つの目安程度にして頂きたい。なお最後の方は手順数が膨大だが、類似の反復が多いだけなので、自分で実際に作図する場合以外は無用に恐れることは無いw
「難易度」は、上の「作図手順数」を参考にしつつも、使った作図手法の分かりやすさなどから、自分の主観で 4 段階で数値化してみた。数字の大きい方が難易度が高いという評価だ。難易度の数字が同じ場合でも、この表の順番で下に行くほど難易度が高いという順にしてある。
最後は「解法」の列について。「外接円/内接円」といった辺りは、中学の幾何辺りで多くの人が既にご存じのもの自体なのでそれを伝えたかっただけ。「方冪の定理/相似形」などは、その考え方を利用しているということ。「○○に帰着」というのは、より難易度の低い問題に変換して解けることを表現した。
・前提として使う定理
作図やそれにあたっての説明のところで必要になる概念や定理で、超基本的な部分は暗黙の了解として完全に省略しているが、円と線が絡む定理で、暗黙の了解として完全に省略していいか迷った事柄だけここで述べておきたい。なお証明は本題から逸れるので略す。多くの皆さんは、「ああそんなのがあったよね」で済むと思うが、気になって落ちつかない方は、検索などすれば幾らでも平易な解説を目にすることができると思う。
「円の直径の端に当たる 2点A , Bと円周上の点Dがあるとすると、∠ADBは直角である」
これは円周角の定理の一種(中心角が180度の場合に該当)である。逆に∠ADBが直角であれば、線分ABは円の直径であるとも言える。一応「円周角の定理」も言っておくと、「円周角は中心角の半分」というものである。下記図で確認して欲しい。もう一つは「方べきの定理」だ。よく使うのは、亜種の接する場合の方。アポロニウスの問題は「円と接する」場合が重要だからだ。「点Pから円に接線を引き、その交点をTとした時、PA・PB=PD・PE=PT^2が成り立つ(※AB^2 とはABの長さの2乗つまり、AB・ABのことを表す)」である。図示すると以下のようになる。元の「方べきの定理」は、「円周上に 4点があり、2点を結ぶ直線の延長がPで交わる時、PA・PB=PD・PEが成り立つ」というものだ。図示すると以下のようになる。こちらは円の中に交点がある場合である。仕事を引退してから、数学やら物理やらを勉強し続けている。一般相対性理論だの量子力学、ガロア理論(群論)などにも挑戦してみたが、ある程度はわかった気になれた程度に留まっている。そして学生の頃からやり切った印象のなかった「アポロニウスの問題」に取り組んでみようと思い立ち、自分なりに納得のいくレベルまで理解できたので、書いてみようと思った次第だ。数学者でも数学の先生でもないので、多々不備はあると思うが、間違いその他気が付いた点は遠慮なくコメントを書き込んでいただいて構わない(すべてに返事できるかは不明だが)。
・アポロニウスの問題とは
アポロニウスの問題とは、平面において、与えられた3つの円に接する円を描く問題のことだ。代数的解法など様々な解法があるが、ここでは、コンパスと定規だけでこの問題を解くことがゴールだ。円を無限に縮小すれば点になり、円の半径を無限大にすることで直線になる。なので、その円の極限の状態を加味する(円と線と点の3種類)ことで、3種類のオブジェクト(円と線と点のこと)の組合せは10種類出来上がる。ここではその10種類すべてをまとめて「アポロニウスの問題」ということにする。
この10種類の問題の中には難易度の低い種類から高い種類まで各種あることが分かっている。ここではその難易度の低い課題から、難易度の高い課題、そして最終的な目的(与えられた3つの円に接する円を描く)に順に辿り、全ての解を作図する手順を示そうというのが、具体的なゴールだ。
・何故その問題を取り上げるのか
実は国内外で様々な人が10種類の個々の問いに答える作図法や動画解説を既に沢山書いている。ではなぜここで私がこの問題を改めて取り上げる必要があるのか?それは、書籍でもウェブサイトでも、これら10種類の課題すべてを順番に丁寧に解説したものを見つけることができなかったからだ。みんなつまみ食いだったり、全部網羅していても、知識の前提レベルが高過ぎて素人にはさっぱり理解できなかったりするのだ。動画は、その瞬間は分かりやすくても、一つ一つ辿って理解したい場合は何度も反復が必要で、やはり紙(静止画)での丁寧な図解がいいのだ。
そこで、ここにその10種類課題すべての作図プロセスを全部自分で解明し、中学校幾何の知識レベルでも理解でき作図できるような資料としてまとめて書くことには大きな意味があると考えたのだ。もちろん専門家ではないので、特に難易度の高い種類の問題で線と円が交わっている場合など、オブジェクトのあらゆる配置の場合を網羅してはいない。あくまでも、典型的な配置の状態での、最も平易な解説が最低限一つ含まれるようにしてあるだけだが、自分で整理するのにも、相当な時間が掛かった。探してもどこにも見つからないはずなので、折角だからその成果を披露しようということだ。中学高校での発展研究課題としても素晴らしい素材になるのではないだろうか。
また解法の種類としては、代数的手法(関数がでてくる)や反転幾何学を使った方法などもあるが、私を含めて素人が、易しく完全にすべてを理解したり、また人に説明できるようなものではないので、取り上げない。易しく説明できるようになった暁には、追記することになるかもしれない。
・「定規とコンパスによる作図」とは
・文章及び作図における表記ルールについて
関連するページ群すべてにおいて、表記ルールは下記に則って書くことにする。

デジタルガレージグループのDGビジネステクノロジーは、「脆弱性対策」の実施を支援する「DGBTセキュリティ診断サービス」の提供を始めた。
2025年3月改訂の「クレジットカード・セキュリティガイドライン6.0版」では、EC加盟店に求めるセキュリティ対策として「脆弱性対策」を追加。「DGBTセキュリティ診断サービス」は、ECサイトの体制やニーズに応じて柔軟に選べる形式で提供する。
対応範囲、緊急度、組織体制、予算に応じて、最適な診断プランを提案する。サービスは大きく3つのメニューで構成する。
クレジットカード不正利用の被害額が過去最悪(2024年は555億円)を更新する環境下、EC事業者にとってセキュリティ対策は事業継続に欠かせない基盤になっている。
ガイドライン6.0では、EC加盟店に求めるセキュリティ対策として「脆弱性対策」の実施を追加。不正利用対策として「EMV3-D」の導入義務化、適切な不正ログイン対策の実施を新たに求めた。
ガイドライン6.0で求めている5項目のセキュリティ対策は、カード情報保護対策として「カード情報非保持化」「脆弱性対策」、不正利用対策として「不正ログイン対策」「EMV3-D」「その他」(加盟店契約上の善良なる管理者の注意義務の履行、オーソリゼーション処理の体制整備)。

なお、「脆弱性対策」では、5項目にわたる技術的対策の実施が求められている。
DGビジネステクノロジーによると、これらの対策のなかでも、Webサイトやシステムに対する脆弱性の発見と対応が、費用や手間、対応範囲の判断といった観点で実務上の負担が大きい領域となっているという。
特に中小規模のEC事業者にとって、セキュリティ専門人材の確保や対策費用の捻出は深刻な課題としている。
※このコンテンツはWebサイト「ネットショップ担当者フォーラム - 通販・ECの業界最新ニュースと実務に役立つ実践的な解説」で公開されている記事のフィードに含まれているものです。
オリジナル記事:「セキュリティガイドライン6.0」で求められる「脆弱性対策」を支援する「DGBTセキュリティ診断サービス」、DGビジネステクノロジー
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.
LINEヤフーは8月以降、「Yahoo!ショッピング」に自社開発のクリック課金型広告、CRMツールといった新機能を段階的に導入する。
プラットフォームの一元化を進めている「Yahoo!ショッピング」では、バリューコマースが出店者向けに提供してきたクリック課金型広告「ストアマッチ」、CRMツール「STORE's R∞(ストアーズ・アールエイト)」を7月31日で終了する。
新機能はそれらに代わる新しいサービスで、広告機能は「Yahoo! JAPAN コマースアドマネージャー」、CRM領域は「ストアクーポン拡張機能」が後継機能になる。
広告機能は「コマースアドマネージャー」が主軸になる。「コマースアドマネージャー」は広告配信の透明性や出稿管理の効率化を目的に設計し、アイテム単位でのターゲティング配信ができる「アイテムリーチ」などを含んでいる。
機能提供元がバリューコマースからLINEヤフーに変わるため、支払い方式も変更。売り上げからの相殺形式に移行し、出店者は利便性の向上が見込まれている。
CRM領域の後継機能である「ストアクーポン拡張機能」は、既存の一括クーポン配布やキャンペーン作成機能などを実装。一部機能(ABテスト・分析ダッシュボードなど)は現段階で継続しないという。
LINEヤフーとバリューコマースは、「StoreMatch」「STORE's R∞」を「Yahoo!ショッピング」向けに提供する取引契約を7月31日で終了。LINEヤフーが「StoreMatch」「STORE's R∞」に代わる新たなサービスを開発するとしていた。
「ストアマッチ」は、バリューコマースが提供するクリック課金型広告。商品単位での広告出稿ができる仕組みで、多くの出店者に利用されてきた。「STORE's R∞」は、CRM支援ツールとしてクーポン配布・ABテスト・定期配信などの機能を実装、顧客ロイヤルティ向上に寄与するツールと言われている。
5月から新機能の提供を順次開始し、旧サービスとの移行期間を設けてきた。旧サービスは7月31日まで利用できる。レポート機能など一部データは自動移行されないため、出店者は事前のバックアップや準備が推奨される。
※このコンテンツはWebサイト「ネットショップ担当者フォーラム - 通販・ECの業界最新ニュースと実務に役立つ実践的な解説」で公開されている記事のフィードに含まれているものです。
オリジナル記事:LINEヤフーの「Yahoo!ショッピング」、「ストアマッチ」「STORE's R∞」の終了で「コマースアドマネジャー」などに移行へ
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.

「モノタロウ」を運営するMonotaROが住設機器の設置工事サービスを始める。7月17日から、「LIXILトイレリフォーム・設置工事サービス」を開始した。
「モノタロウ」ではこれまで、トイレなど住設機器は販売のみで、購入顧客はリフォーム会社などに設置工事を依頼する必要があった。こうした課題を解決するため、設置工事まで手がける「LIXILトイレリフォーム・設置工事サービス」を開始した。
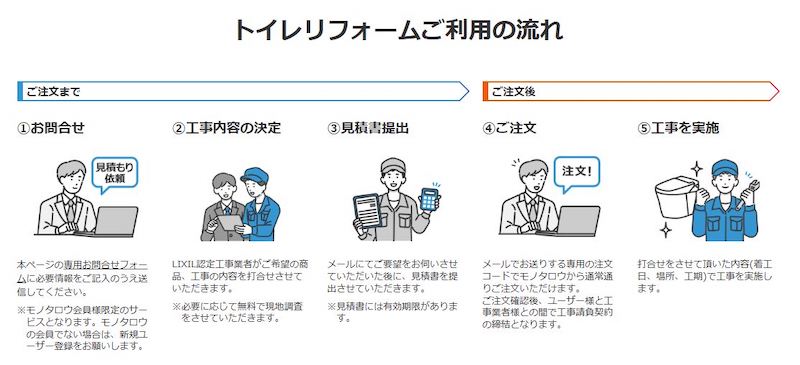
「LIXILトイレリフォーム・設置工事サービス」は、ECサイト「モノタロウ」の法人会員向けに提供。実績が豊富なリフォーム会社と提携し、一部地域を除く全国での設置工事に対応する。専門スタッフが商品選定のサポートから納品場所や納品日について顧客と個別に打ち合わせし、円滑な設置工事を提供するとしている。
利用の流れは次の通り。
※このコンテンツはWebサイト「ネットショップ担当者フォーラム - 通販・ECの業界最新ニュースと実務に役立つ実践的な解説」で公開されている記事のフィードに含まれているものです。
オリジナル記事:モノタロウ、住設機器の設置工事サービスを開始、LIXILトイレリフォームの設置に対応
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.

堀江貴文氏がファウンダーのロケット事業や通信衛生事業を手がけるインターステラテクノロジズは7月10日、第三者割当増資と金融機関の融資により89億円を調達したと発表した。第三者割当増資の引受先にはジャパネットホールディングスも名を連ねている。
インターステラテクノロジズは、三井住友銀行、スパークス・アセット・マネジメントが運用する宇宙フロンティア2号ファンド、ジャパネットホールディングスと既存株主を引受先とした65億円の第三者割当増資、金融機関からの24億円の融資で89億円を調達した。
ジャパネットグループは2019年、通信販売事業に並ぶ柱としてスポーツ創生域創生事業を加え、2024年10月に開業した長崎スタシティシティを中心に地元の崎で創生域創生を進めている。インターステラテクノロジズが推進する宇宙産業による振興創生の取り組みは、ジャパネットグループの事業とも共通点が多く、理念に共感する部分があり出資を決めたという。
インターステラテクノロジズが取り組む⼈工衛星の打ち上げを通じた国内における宇宙産業の振興、北海道⼤樹町における創生域取り組みり組みは、地域に新たな産業を創り出すという点で、ジャパネット創生域創生事業とも共通点が多く、理念に共感する部分があり、出資を決定した。日本の未来を担創生域創生と宇宙産業の発展を後押しできればと思う。(ジャパネットホールディングス 髙田旭人社長)
※このコンテンツはWebサイト「ネットショップ担当者フォーラム - 通販・ECの業界最新ニュースと実務に役立つ実践的な解説」で公開されている記事のフィードに含まれているものです。
オリジナル記事:ジャパネットがロケット事業に進出? 堀江貴文氏がファウンダーのインターステラテクノロジズに出資
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.

楽天グループの三木谷浩史会長兼社長最高執行役員は7月18日、X(旧Twitter)で7月20日投開票の参院選に国民民主党から比例代表に立候補している元楽天社員について、「eコマース推進が大きな政策の柱」「ふるさと納税のポイント付与禁止にも、真っ向から反対」と言及した。
比例代表に立候補しているのは新人の小野貴樹氏。楽天グループで社長室兼渉外室政務課シニアマネージャー、楽天モバイルで政策推進室長、新経済連盟で政策部副部長を務めた経歴を持つ。三木谷氏のXによると、小野氏とは規制改革、日本の経済成長論を議論し合った仲という。
小野貴樹氏は政策で、「ふるさと納税へのポイント付与禁止に反対」のほか、「所得倍増6か年計画」を掲げ、減税による手取り増加、ふるさと納税再生と地方活性化などをあげている。
なお、三木谷社長は7月17日、選挙の期日前投票を社員ができるように、18日午前を「特別休暇」にするとXで公表。投票日が3連休の中日にあたることを踏まえた対応という。
ふるさと納税に関して楽天グループは7月10日、ふるさと納税のポータルサイトで寄付に対してポイント付与を全面的に禁止する総務省の告示は違法であるとして、国を相手取り、告示の無効確認などを求める行政訴訟を東京地方裁判所に提起したと発表。「国会の議論を経ずに告示1つでルールを変えるのは、法治国家としておかしいのではないか」などとし、行政手続きの正当性を問う姿勢を示している。
※このコンテンツはWebサイト「ネットショップ担当者フォーラム - 通販・ECの業界最新ニュースと実務に役立つ実践的な解説」で公開されている記事のフィードに含まれているものです。
オリジナル記事:楽天・三木谷社長、元社員の参院選立候補者に「eコマース推進が大きな政策の柱」「ふるさと納税のポイント付与禁止にも、真っ向から反対」と言及
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.

Kivaは7月16日、事業者向けのワークフロー型AIエージェント「SAMURAI(サムライ)」の提供を開始した。AIがPCを直接操作し、導入企業の業務効率化をサポートする。ECサイト運営の商品登録、競合・営業先の分析などの利用シーンを想定しているという。

「SAMURAI」は、ユーザーが自然言語で業務ワークフローを作成すると、その内容に基づきAIがPC画面上のGUI操作を自動で実行する。ブラウザ操作、生成AIモデル間の連携を標準化するためのプロトコルであるMCP連携を中心に対応。今後はPC全体の操作にも対応を予定している。
従来のチャット指示型AIとは異なり、都度の入力や確認を必要とせず、あらかじめ自然言語で指示した内容に従って「SAMURAI」が自律的に業務を進行する。
現代人の業務は、作業的にPCを操作することにリソースを取られやすく、本来時間を割きたいはずの“考える作業”がひっ迫されている。
こうした課題を解決するため、AIを人間が生き抜くための知的な“刀”とするべきだと考えた。「SAMURAI」はAIがPCを自律的に操作する、言わば新たな業務インフラとなる。(代表取締役会長 野尻航太)
「SAMURAI」の新サービス発表会に登壇したKivaの代表取締役会長 野尻 航太氏
「SAMURAI」の活用が見込まれるシーンは、ECサイト運営の商品登録、競合・営業先の分析、資料作成、メールチェック・送信、商談調整、新入社員のアカウント発行など。
月額費用は、「ビジネスプラン」は2万9800円。上位プランとなる「エンタープライズプラン」は応相談となる。このほか、個人の利用にも対応する(個人利用は無料)。
また、企業のAI活用で一般的に懸念されることが多いセキュリティに関しては、「導入企業のセキュリティの認識の要件を満たせるようにしている」(野尻氏)
※このコンテンツはWebサイト「ネットショップ担当者フォーラム - 通販・ECの業界最新ニュースと実務に役立つ実践的な解説」で公開されている記事のフィードに含まれているものです。
オリジナル記事:Kiva、ワークフロー型AIエージェントを提供開始。ECの商品登録などを自動で実行、業務効率化を支援
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.


楽天が「ふるさと納税」のポイント禁止で国を提訴。総務省の告示は「官民連携の努力や工夫を一方的に否定するもの」

【テレビ通販大手3社の2024年度】売上高はショップチャンネルが1677億円、QVCは1317億円、ジャパネットHDは2725億円
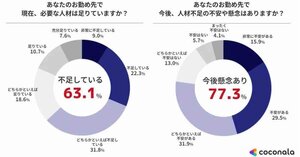
企業の人材不足、「不安や懸念を感じる」は77%。最も不足している職種は「IT部門」、対策は「採用」「定年の延長」など

漫画ECのTORICO、ビットコイン投資など暗号資産事業に進出
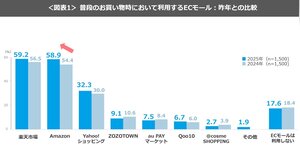
普段使うECモールの1位は「楽天市場」、2位「Amazon」、3位「Yahoo!ショッピング」、4位「ZOZOTOWN」、5位「au Payマーケット」

Amazonの物流ロボット100万台目が日本で導入、アマゾンが進めるAIを活用した物流革新
「楽天市場」でパーソナライズド検索がスタート、ユーザーごとに検索結果を最適化
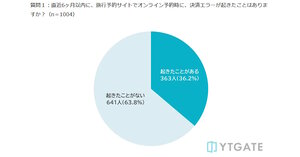
決済トラブルに36%が経験。2割が購入断念、7割が他サイトへ流出【旅行・チケット予約の決済調査】
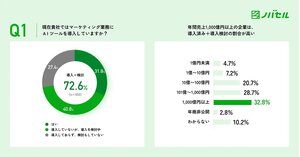
マーケターの7割がAI活用・導入に前向き。導入済企業は約3割。強化したい領域は「分析・インサイト抽出」が最多
「SmartNews」への広告掲載、自社で出稿・運用できる新機能「セルフサーブ型広告」をリリース
※期間内のPV数によるランキングです。一部のまとめ記事や殿堂入り記事はランキング集計から除外されています。
※このコンテンツはWebサイト「ネットショップ担当者フォーラム - 通販・ECの業界最新ニュースと実務に役立つ実践的な解説」で公開されている記事のフィードに含まれているものです。
オリジナル記事:楽天が「ふるさと納税」のポイント禁止で国を提訴/テレビ通販大手3社の2024年度の売上高は?【ネッ担アクセスランキング】 | 週間人気記事ランキング
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.

ヘアケアブランド「SILK THE RICH」のTHE RICHは7月17日、堀江貴文氏が率いるHIUインベストメントから“異例の規模”で資金調達を実施したと発表した。
HIUインベストメントによる大型出資の背景について堀江氏は、「SILK THE RICH」の独自性とスケーラビリティの高さに注目し、スタートアップへの投資としては過去最大規模の支援を決断したとしている。今回の出資を機に、堀江氏は経営・マーケティング・PRの各面で深く関与していくという。

「SILK THE RICH」はシルクの再生補修成分を配合したD2Cヘアケアブランド。シルク特有のツヤと指通りを実現する高い補修・保湿効果を持つ製品という。通常のヘアケア製品の約2倍の香料を配合し、翌日までリッチな香りが持続するところも特長。「価格」よりも「品質」を重視したブランドコンセプトとし、日本のシルクを世界に広めることを目指しているという。
サブスクリプション継続率は97%を超え、製品を扱う実店舗は国内で約1万店まで広がっている。年内には18か国へのグローバル進出を予定する。
THE RICHは格闘家の朝倉未来氏が2023年7月に出資して取締役に就任。2025年6月には売れるネット広告社と国内における「TikTok Shop」独占運営を中心とした戦略業務提携を締結している。
調達資金の主な使途と今後の展開は、グローバル・サブスクリプション・リテールの三軸で進めていくという。

日本発で世界に通用するD2Cブランドがもっと出てくるべきだと思っていた。「シルクザリッチ」は、素材、商品力、世界観、そのすべてに可能性がある。三浦氏の突き抜けた推進力にも期待しているし、本気でユニコーン、いや“デカコーン”をめざせるブランドだと信じている。だからこそ、HIUインベストメント史上でも異例の規模で出資し、私自身も経営・発信・連携を通じて企業価値の最大化に直接関わっていく。(堀江貴文氏)
堀江貴文氏
※このコンテンツはWebサイト「ネットショップ担当者フォーラム - 通販・ECの業界最新ニュースと実務に役立つ実践的な解説」で公開されている記事のフィードに含まれているものです。
オリジナル記事:ヘアケアブランド「SILK THE RICH」のTHE RICH、堀江貴文氏のHIUインベストメントから“異例の規模”で資金調達
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.

デジタルコマースに関わる事業者必見のオンラインイベント「Digital Commerce Frontier 2025」を7月29日(火)+30日(水)に開催します。セブン-イレブン・ジャパン、ZOZO、中川政七商店、アスクル、パルコ、アシックス、ワコール、スマートニュースなど、著名企業の成功事例や実践的な知見を学べるさまざまなセッションを用意。リテールビジネス、BtoC-EC、BtoB-EC、メーカーECなどデジタルコマースに携わる事業者を対象に、AIやリテールテックなどの最新トレンド、最先端テクノロジー活用、事例、最新ソリューションなどをお届けします。視聴はすべて無料です!(事前登録制)。まだお申し込みをしていない方のために、編集部がおすすめ講演の見どころをご紹介します。
7月29日(火)11:00~11:45 KB1-1オープニング基調講演
アスクルは、2025年5月期までの中期計画で「すべての仕事場とくらしを支えるインフラ企業」になることを掲げていました。この達成にむけて、BtoB事業においてマーケティングがどのような役割を担ってきたのかについて、認知・購買・初期稼働・リテンション・ロイヤル化といったお客さまのフェーズごとに事例を交えながら紹介します。

アスクル株式会社 プロダクト&マーケティング本部 マーケティング 統括部長 高城 梨理世氏
2010年大手インターネット企業に新卒入社。広告事業領域での商品企画・開発業務を経て、2014年より予約型広告の責任者として従事。その後、ベンチャー企業で企画業務全般やプロダクトオーナーの経験を積み、2016年12月にアスクル入社。BtoC事業の事業企画業務やマーケティング業務に従事した後、2023年3月よりBtoB・BtoC両事業のプロモーション領域を統括。2025年5月より現職にて、BtoB・BtoC両事業のマーケティング全般を統括。
セッションでは、アスクルさん社内におけるマーケティングの役割を解説。マーケティング活動全体図における「認知」の段階ではリアルイベント開催、初回購入時にはメール施策など、ユーザーのフェーズごとにどのような施策を行い成果を上げているのか、具体的な取り組みと合わせて解説します。
7月29日(火)14:00~14:45 KB1-4特別講演
「2025年法人向け通販サービス顧客満足度調査」の結果をもとに、BtoB通販における顧客満足度向上のための重要なポイントを解説。また、EC事業者のSDGsへの取り組みに対する顧客意識や評価についても、最新データを交えてご紹介します。BtoB-ECを運営する企業にとって、顧客満足度向上とSDGsへの取り組みは重要な課題。J.D. パワーの調査結果から得られる知見を通じて、実践的な改善策を学べる貴重なセッションです。

株式会社J.D. パワー ジャパン Global Business Intelligence部門 通信・テクノロジーサービスインダストリー シニア ディレクター 野本 達郎氏
日本総合研究所を経て、2007年J.D. パワー ジャパンに入社。入社以来、主に情報通信分野における顧客満足度調査の企画立案・分析に従事。現在、J.D. パワーの日本国内におけるIT・情報通信業界、オフィスサービス業界向け事業を統括。
7月に公表予定の「2025年法人向け通販サービス顧客満足度調査」の最新情報から、BtoB通販で顧客満足度を向上させるためのポイントを学ぶことができます。「法人向け通販サービス顧客満足度調査」はJ.D. パワー ジャパンが毎年公表している、法人向け通販に関する調査報告書。全国の事業所を対象に、法人向け通販サービスの利用状況や各種経験、満足度を聴取しています。この調査結果をベースにしたセッションから、どのようなファクターが顧客満足度に直結するのかといった、法人向け通販サービスの改善策を学ぶことができます。
次回はまた別のオススメ講演をお伝えします!
※このコンテンツはWebサイト「ネットショップ担当者フォーラム - 通販・ECの業界最新ニュースと実務に役立つ実践的な解説」で公開されている記事のフィードに含まれているものです。
オリジナル記事:アスクルのBtoB-ECマーケティング施策、顧客満足度向上のポイントが学べるオンラインECセミナー【7/29+30開催】
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.
TSIホールディングスは7月14日、デイトナ・インターナショナルを買収すると発表した。取得価額は283億円。
デイトナは「FREAK'S STORE」などのリアル店舗、自社ECサイト「DAYTONA PARK」を展開し、カジュアル・スポーツ・アウトドアなど幅広いシーンをカバーした商品・サービスを展開している。
2025年2月期業績は売上高が前期比10.2%増の393億3900万円、営業利益は5億3900万円(前期は1億5000万円の赤字)、経常利益は3億6700万円(同7億2700万円の赤字)、当期純損益は7000万円の赤字(同9億6300万円の赤字)だった。
TSIはデイトナの買収について、ブランドポートフォリオが大きく拡充できることにメリットがあると説明。比較的狭いゾーンにブランド展開が集中しているTSIにとって、カバーしきれていない分野を有効に埋められる強みがあり、成長戦略に合致するとしている。
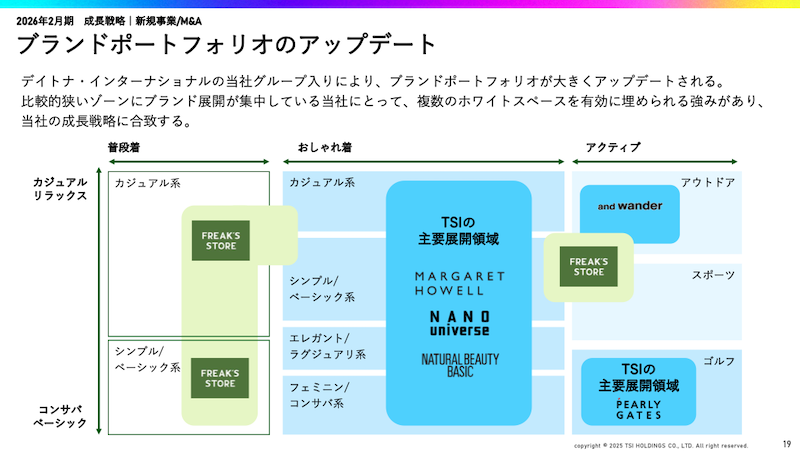
またデイトナはブランドポートフォリオだけではなく、TSIに不足している領域に多くの強みや特長を持つことから、相互補完関係を期待することができると判断。シナジー効果が期待できるとした。具体的に想定しているシナジー効果は次の通り。
マーケット領域として、カジュアル、スポーツ、アウトドアなどTSIにとって空白だった領域を幅広くカバー。また顧客層としては20代を中心とした若年層の取り込みを図る。店舗網として、地方都市のショッピングセンターなどを含め全国をカバーする。
アクティブユーザー数約80万人のECサイト「Daytona Park」と、TSIの「mix.tokyo」とのシナジーを追求する。
連結仕入高が30%前後のスケールアップを見込み、仕入原価に関する構造改革のスケールメリットを拡大できる可能性があるとした。
DXソリューション事業の成長ポテンシャルに高い期待があり、TSI既存事業での積極的な活用を推進するとしている。

今回の買収ではデイトナの「Daytona Park」と、TSIの「mix.tokyo」とのシナジーを追求するとしているが、ECプラットフォームの動向について注目が集まりそうだ。
デイトナは2022年11月に自社ECサイト「FREAK'S STORE ONLINE SHOP」のコンセプトとデザインをリニューアルし、特定ブランドに偏らないECモール「Daytona Park」として刷新。TSIは2025年2月、30超のブランドのEC基盤を「Shopify」へ統合、公式EC「mix.tokyo」も「Shopify Plus」でリニューアルしている。
※このコンテンツはWebサイト「ネットショップ担当者フォーラム - 通販・ECの業界最新ニュースと実務に役立つ実践的な解説」で公開されている記事のフィードに含まれているものです。
オリジナル記事:TSIホールディングス、デイトナを買収。期待されるシナジー効果は? ECプラットフォームはどうなる?
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.

ワールド子会社のティンパンアレイは7月16日、ユーズドセレクトショップ「RAGTAG(ラグタグ)」の海外1号店を、タイ・バンコクの中心に位置する大型商業施設「One Bangkok」にオープンした。
ワールドとタイの企業グループSAHA GROUP(サハグループ)が2025年1月に設立した合弁会社WORLD SAHA(THAILAND)CO.,LTD.が出店を担った。今後はタイおよびASEAN市場で「RAGTAG」の事業基盤を築き、市場ニーズに応じた事業を展開する。

ティンパンアレイが運営する「RAGTAG」は、日本国内で24店舗を運営しており、EC販路も展開。5000以上のデザイナーズアイテムを厳選して提供している。
タイにおける二次流通の展開に向けて、ワールドから経営人材を派遣。ティンパンアレイが現地での店作りと販売ノウハウ面で人材の育成を進めてきたという。
また、SAHA GROUPのネットワークを活用した物流管理や、ラグジュアリー商材の仕入れを強化した。

タイでは自社ECと実店舗との連携を強化する。国内の「RAGTAG」でも利用者が多い店舗取り寄せ機能、観光が盛んなバンコクにおける観光客向けの販売戦略も視野に入れ、オウンドメディアなどを通じて「RAGTAG」の認知を広げる。

2024年の春にタイで開催した「ラグタグ」のポップアップでは、現地の売れ筋ブランド、サイズ、価格帯を把握することができたという。今後はニーズを捉えながら、タイだけでなくASEAN市場全体においても早期の事業基盤確立をめざす。
※このコンテンツはWebサイト「ネットショップ担当者フォーラム - 通販・ECの業界最新ニュースと実務に役立つ実践的な解説」で公開されている記事のフィードに含まれているものです。
オリジナル記事:ワールドグループ、ユーズドセレクトショップ「RAGTAG」の海外1号店をタイで開店
Copyright (C) IMPRESS CORPORATION, an Impress Group company. All rights reserved.