アユムさん、このA4のチラシをA3に拡大コピーしてもらえるかな。
ところで、A4からA3にするのって、何倍にすればいいんだっけ。
先輩、そんな細かいことは気にしなくても、コピー機が全部やってくれますから大丈夫です。でも、感覚的には2倍って感じがします。
え、待ってください! A3サイズの半分がA4サイズなら、2倍にすればいいんじゃないんですか? なんで1.41倍なんですか? 先輩~!
昔から、算数も数学も苦手なアユムは、希望が叶ってマーケティング部門に異動してきました。Web担で見るような「すごいマーケターになりたい!」と胸を躍らせていたが、配属後、理想と現実のギャップに苛まれることに。データ、数字、%、小数。うわぁーん、どうしたら、数字に強くなれるのでしょうか……。
そこに現れたのが、大人向け数学教室「大人塾」を運営し、数学苦手な社会人に対して指導をしているアジアゾウをこよなく愛するモリさん。
この記事を読むべき人:比率の計算が苦手な方
この記事を読む必要がない人:比率の計算ができる方
この記事でわかること:縮小・拡大の比率
拡大・縮小の計算
モリさーん、A4の紙をA3に拡大コピーするとき、1.41倍って本当ですか?
先輩がそう言うんです。でも、A3はA4の2枚分だから、2倍じゃないですか?モリさんはどう思いますか。
どう思うって言われても……。確かに、計算すると1.41倍ですね。先輩が正しいです。
モリさんも1.41倍だと思いましたか。どう計算するのですか?
思ってるというか、計算するとそうなったんですが……。まず、A判サイズの紙について確認します。A3サイズの半分がA4サイズです。A3サイズとA4サイズの縦横比は同じです。
図にするとこんな感じです。
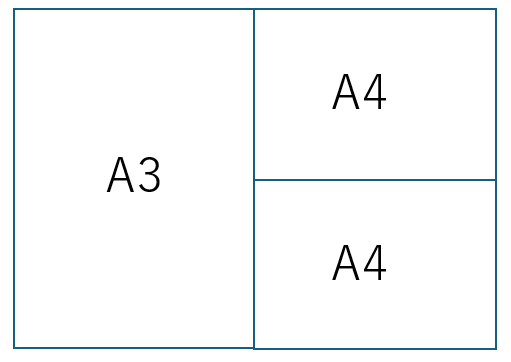
はい。A4はA3サイズの半分ですよね。だから、2倍に拡大するのだと思ってました。
その気持ち、ちょっとわかります。でも、少し立ち止まって考えてみましょう。A4を2枚並べるとA3になりますよね。
では、試しに長さを2倍にしてみましょう。A4の縦と横をそれぞれ2倍に拡大すると……、図で見てみますか。

そうなんです。縦を2倍、横を2倍にすると、面積は2×2で4倍になり、A3より大きくなります。
なるほど! A4をA3に拡大するときは、面積が2倍になってほしいけど、長さを2倍にしちゃうと面積は4倍になっちゃうんですね。面積と長さの倍率って違うんだ……。
その通りです。では、面積を2倍にするには、長さを何倍にすればいいのか、計算で求めていきましょう。
倍率を求めるためには、それぞれの長さが必要ですよね。
縦と横の比率だけなら、長さがわからなくても求められます。そして、比率が分かれば、倍率がわかります。
そんな魔法みたいなことが……。どういうことでしょう。
たとえば、A4サイズの、短辺の長さを「1」、長辺の長さを「a」としましょう。
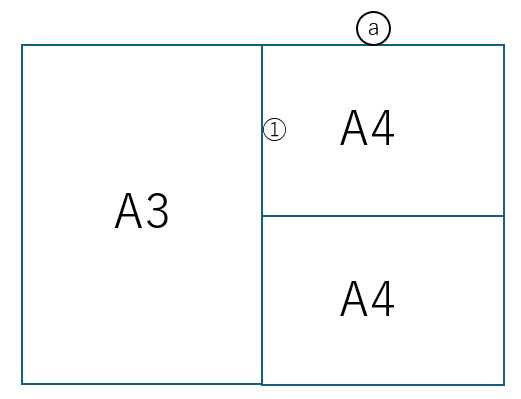
となると。A3の長辺の長さはどのように表せますか。
A4の長辺とA3の短辺は同じ長さなので、aですね?
その通りです。つまり、「A4サイズの短辺の長さ:長辺の長さ」は、「1:a」と表すことができます。そしてA3サイズは「a:2」と表せますね。
比ですね。比については、森さんの書いた『コレ解ける? 数字がこわくなくなる おとな算数ゆるトレ』で詳しく書いてあったのを読みました!
では復習です。 A:B = C:D のとき、AD = BC という式が成り立つのでした。
A4サイズとA3サイズの縦横の長さの比率は同じですので、1:a = a:2 と表せます。
ここで使うんですね! 計算すると、 a² = 2
2乗が出てきました。
ここからaの値を求めます。a² = 2 ですから……
えーと、2乗して2になる数って…… あ! √2ですか?
その通りです! √(ルート)の記号、覚えてましたか?
ひっさしぶりです! 2乗したら2になる数が√2ですよね。
その通りです。では、√2を小数で表したときの数値は覚えてますか?
えーと、ひとひとひとって3回書いて飲みこむっぽいやつでしたよね。
ちょっと違いますが、ひとよひとよにひとみごろ、1.41421356…でしたね。
そうそう! それ! √3がひとなみにおごれや(1.7320508…)でした!
A判サイズの縦横比率は、1 : √2、1 : 約1.41ということです。%で表したときに100倍するので、小数第2位まで表示させています。
ということは……A4の短辺を1とすると、長辺が1.41。そしてA3の短辺がA4の長辺と同じ1.41で、A3の長辺が2ってことですよね。
そっか! A4の短辺1を基準にすると、A3の短辺は1.41になる。だから、A4の縦横をそれぞれ1.41倍すれば、ちょうどA3サイズになるんですね!
そうです。このとき面積は 1.41×1.41 ≒ 2倍 になります。縦横の長さをそれぞれ1.41倍すれば、A4サイズはA3サイズになるわけです。
なるほど! 面積と長さの関係がやっと理解できました。じゃあ、逆のA3からA4への縮小は?
縮小の場合は考え方を逆にします。A3の縦横比は1.41:1ですね。この1.41を1としたとき、1の方をbとおくと、1:bと表せます。
そうか。1.41:1 = 1:b となるわけですか。
このbを求めると 1.41b = 1
b = 1÷1.41 ≒ 0.709 ≒ 0.71
あ、先輩の言っていた縮小の倍率になりました。先輩は、合ってた!
A5サイズをA3サイズに拡大しよう
それでは、A5サイズをA3サイズに拡大するときには、何倍にすればいいですか?
図で確認します。A5サイズはA3サイズの半分の半分、つまり4分の1の大きさですね。また、A4の短辺を「1」としたとき、A5の長辺は「1」、A3の長辺は「2」となります。
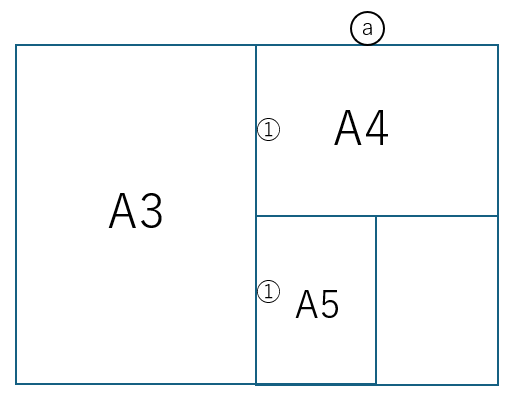
そっか、A3の長辺はA5の長辺の2倍だから、A5からA3にするときは、2倍にすればいいんですね!
その通りです。
A5→A4は、√2 ≒ 1.41倍
A4→A3は、√2 ≒ 1.41倍
なので、A5→A3は、√2×√2 = 2
つまり、2倍であることが分かります。
ここで2倍なんですね。ということは、A3から、A5 にするときには、半分の0.5倍、50%にすればいいということか。
コピー機に頼りっぱなしじゃなくて、仕組みを理解しておくと面白いですね。
そうですね。比率は生活によく使われますから、うまく使いこなしていきましょう。
ポイント
A判のサイズが1つ大きくなる(例:A4 → A3)または小さくなる(例:A3 → A4)とき、面積は2倍または1/2倍になりますが、長さ(辺)の倍率は以下のようになります。
拡大(例:A4 → A3、A5 → A4)
- 長さ(縦・横)の倍率: √2倍
- √2 ≒ 1.414
- コピー機の設定では「141%」が使われます。
縮小(例:A3 → A4、A4 → A5)
- 長さ(縦・横)の倍率: 1/√2倍
- 1/√2 ≒ 0.707
- コピー機の設定では「70%」または「71%」が使われます。
今日の復習
Q1. A4サイズの資料をA3サイズに拡大コピーするとき、何%に設定すればよいですか?
A4→A3 は 縦横をそれぞれ √2 倍 にする
√2 ≒ 1.41
1.41×100 = 141%
答え:141%
Q2. A3サイズの資料をA4サイズに縮小コピーするとき、何%に設定すればよいですか?
A3→A4 は 縦横を 1/√2 倍 にする
1÷√2 ≒ 0.707
0.707×100 = 70.7%→71%
答え:71%
Q3. A5サイズの資料をA3サイズに拡大コピーするとき、何%に設定すればよいですか?
A5→A4 は√2 倍(1.41倍)
A4→A3 も√2 倍(1.41倍)
√2×√2 = 2倍
2×100 = 200%
答え:200%